Question

Бісектриса прямого кутаділить гіпотенузу прямокутного трикутника на відрізки, різниця яких складає 5 см. Знайдіть площу трикутника, якщо його катети відносяться як 3:4.​

Answer 1

Задача: Биссектриса прямого угла делит гипотенузу прямоугольного треугольника на отрезки, разность которых составляет 5 см. Найдите площадь треугольника, если его катеты относятся как 3:4.

Решение:

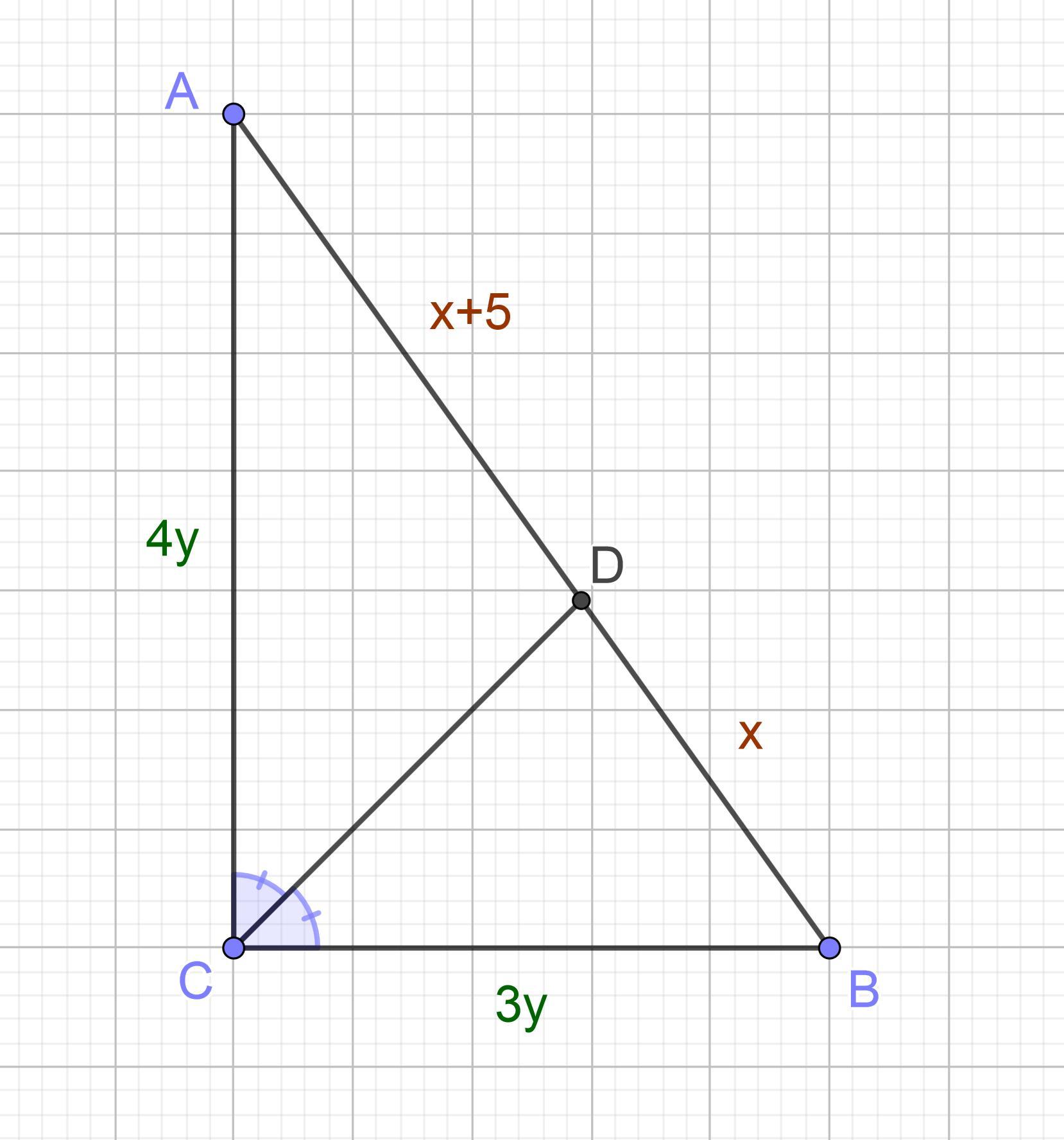
Пусть дан ΔABC, ∠C = 90°, CD — биссектриса. Исходя из условия задачи, обозначим длины отрезков AD за x+5 (см), BD за x (см), AC за 4y (см), BC за 3y (см).

Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника:

    $\frac{AD}{AC} =\frac{BD}{DC} \\\\\frac{x+5}{4y} = \frac{x}{3y} \\\\4y\cdot x = 3y(x+5)\\\\4yx = 3yx+15y\\\\yx=15y\\\\x=\frac{15y}{y} = 15 \:\: (cm)$

    $BD = x = 15 \:\: (cm)\\AD = x+5 = 15+5 = 20 \:\: (cm) \\AB = AD+BD = 20+15 = 35 \:\: (cm)$

Применим т. Пифагора для определения переменной y:

    $AB^2=AC^2+BC^2\\(4y)^2+(3y)^2 = 35^2\\16y^2+9y^2 = 1225\\25y^2=1225\\y^2= \frac{1225}{25} = 49\\y = |y| = 7$

    $AC = 4y = 4\cdot 7 = 28 \:\: (cm)\\BC = 3y = 3\cdot 7 = 21 \:\: (cm)$

Подставим значения в формулу площади прямоугольного треугольника:

    $S_{ABC} = \frac{a\cdot b}{2} = \frac{AC\cdot BC}{2} = \frac{28\cdot 21}{2} =14\cdot 21 = 294 \:\: (cm^2)$

Ответ: Площадь треугольника равна 294 см².