Question

В равнобедренном треугольнике к боковой стороне проведена высота и биссектриса угла, прилежащего к основанию. Определи угол между высотой и биссектрисой, если угол вершины ∡ B = 42°. ∡ MAN = °.

Answer 1

Ответ:

13,5°

Объяснение:

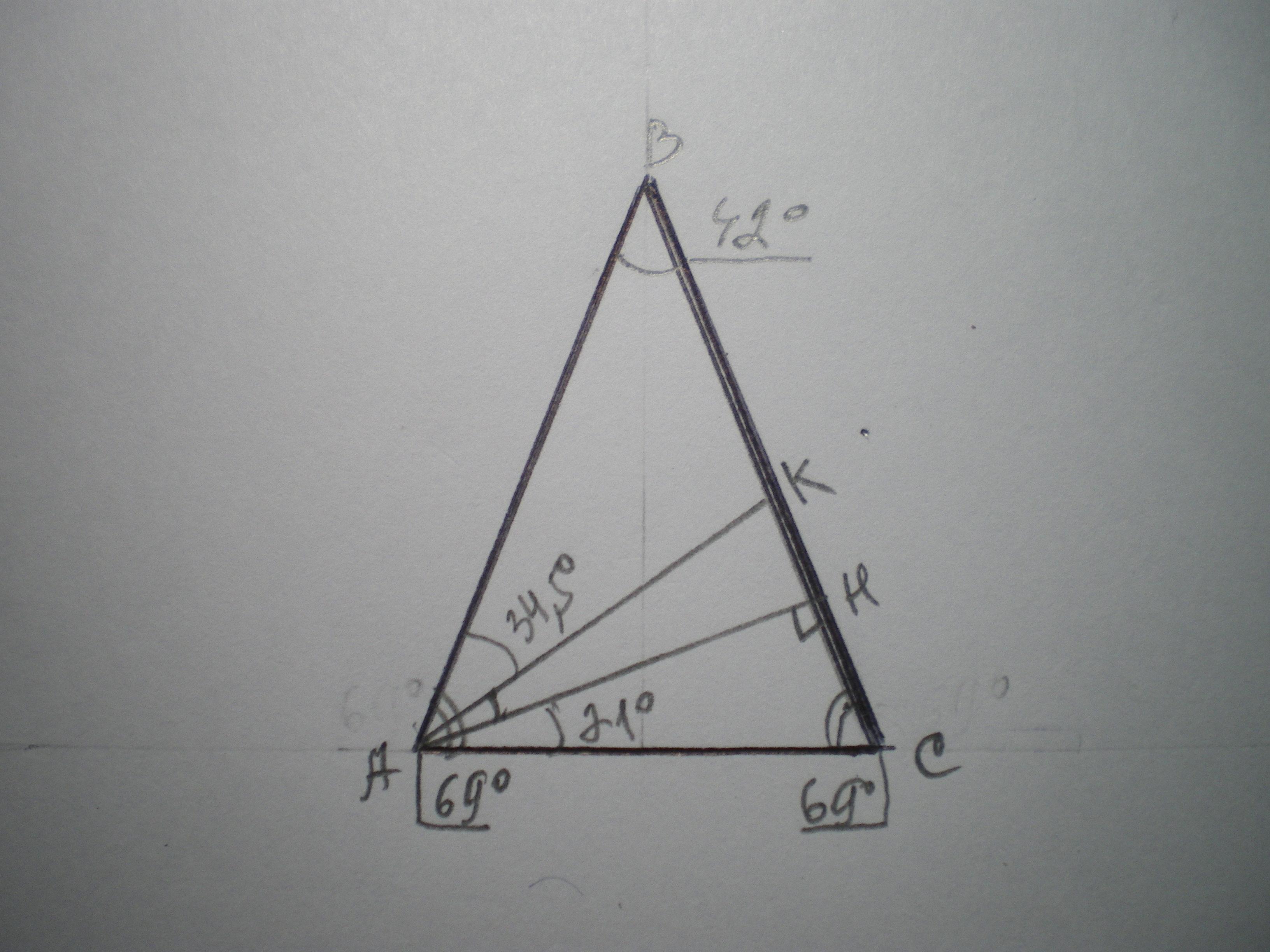
Дано: ΔАВС, АВ=ВС, ∡В=42°,  АН - высота, АК - биссектриса. Найти ∡НАК.

В равнобедренном треугольнике углы при основании равны, поэтому ∠С=∠ВАС=(180-42):2=69°

ΔСАН - прямоугольный, ∠СНА=90°, ∠НАС=90-69=21°, т.к. сумма острых углов прямоугольного треугольника составляет 90°.

∡КАС=1/2 ∡ВАС=69:2=34,5°

∡НАК=34,5-21=13,5°