Question

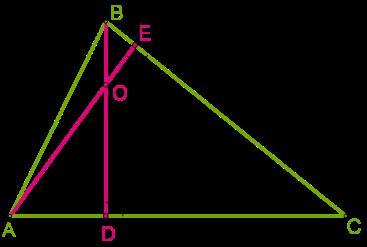
Высоты треугольника пересекаются в точке O.
Величина угла ∡ BAC = 74°, величина угла ∡ ABC = 86°.
Определи угол ∡ AOB.

Answer 1

Ответ:

<АОВ=160°

Объяснение:

∆АВЕ прямоугольный, <ВАЕ=180°-90°-86°=4° по сумме углов в∆

∆ABD прямоугольной

<АВD=180°-90°-74°=16° по сумме углов в∆

∆АОВ в нем знаем 2 угла, найдем

<АОВ=180°-16°-4°=160° по сумме углов в ∆

Answer 2

Решение:

Р-м Δ ABE:

∡AEB = 90°, ∡ABE = 86° (∡ABE ∈ ∡ABC).

Исходя из теоремы о сумме углов треугольника, градусная мера ∡BAE будет равна:

∡BAE = 180−(∡AEB+∡ABE)=180−(90+86) = 180−176 = 4°.

Р-м Δ ABD:

∡ADB = 90°, ∡BAD = 74° (∡BAD ∈ ∡BAC)

Исходя из теоремы о сумме углов треугольника, градусная мера ∡ABD будет равна:

∡ABD = 180−(∡ADB+∡BAD) = 180−(90+74) =180−164 = 16°.

По аналогии, угол ∡AOB в Δ ABO равен:  

∡AOB = 180−(∡BAO+ABO) = 180−(4+16) = 180−20 = 160°

Ответ:  ∡AOB = 160°.