Предмет: Геометрия, автор: nykablin

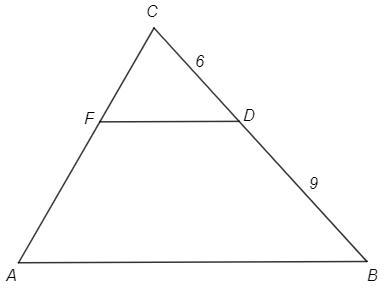
Прямая параллельная стороне AB треугольника ABC, пересекает его сторону AC в точке F, а сторону BC с точке D. Найдите площадь трапеции AFDB, если CD=6 см, DB=9 см, а площадь треугольника FCD=20 см2.

Ответы

Автор ответа: siestarjoki

△ACB~△FCD (по соответственным углам при FD||AB)

S(ACB)/S(FCD) =k^2 =(15/6)^2 =25/4

S(AFDB)/S(FCD) =21/4

S(AFDB) =20*21/4 =105 (см^2)

Приложения:

siestarjoki: k=CB/CD=15/6

siestarjoki: Треугольники ACB и FCD подобны, коэффициент подобия равен отношению сходственных (т.е. лежащих против равных углов) сторон.

siestarjoki: Отношение площадей подобных фигур равно квадрату коэффициента подобия.

karmaakabane04: Срочно надо, пожалуйста!!!
Как ты в предпоследней строчке:
""S(AFDB)/S(FCD) =21/4""
Нашел 21 на 4?? Очень срочно надо, буду безумно благодарен тебе за это. Мне приммером надо как ты это получил

karmaakabane04: И как получилась последняя строчка с 20. Если поможешь, то буду очень благодарен и поставлю 5 баллов вместе с "спасибо"

siestarjoki: S(ACB)/S(FCD) =25/4
S(ACB)=25x, S(FCD)=4x
S(AFDB)=S(ACB)-S(FCD)=25x-4x=21x
S(AFDB)/S(FCD) =21x/4x =21/4

siestarjoki: S(AFDB)=21/4 *S(FCD)=20*21/4

yzagumennikov: можешь видос записать

yzagumennikov: не понял как ты решил

yzagumennikov: 25 придурок как ты получил

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Русский язык, автор: mssheleketo

ПОДЧЕРКНИ СЛОВА. КОТОРЫЕ ВЕРНО РАЗДЕЛЕНЫ НА СЛОГИ. МА-ЛЫ-ШИ.У-ТЮГ. К-РОТ. КО-РО-ВА. СТ-РА-УС.У-ЖИ-Н. ПО-МИ-ДОР. ЗА-НОЗА. СА-ПО-ГИ.ТЕТ-РА-ДЬ. ЛО-ПА-ТА. ЛЕ-НЬ. ЗА-ВО-ДЫ.

2 года назад