Question

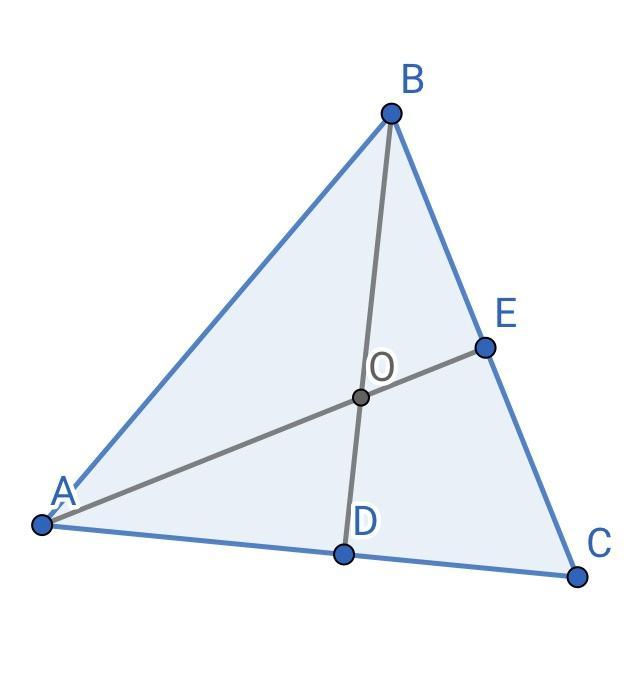
Высоты треугольника пересекаются в точке O.
Величина угла ∡ BAC = 53°, величина угла ∡ ABC = 63°.
Определи угол ∡ AOB.

∡ AOB =
°.

Answer 1

Дан △АВС.

Проведём две высоты: AE и BD.

АЕ и BD ∩ = O, по условию.

Так как BD - высота ⇒ △ABD - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ABD = 90˚ - ∠ВАС = 90° - 53° = 37˚

Так как АЕ - высота ⇒ △ВАЕ - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ВАЕ = 90° - ∠АВС = 90° - 63° = 27°

Рассмотрим △АОВ:

Сумма внутренних углов треугольника равна 180°.

⇒ ∠АОВ = 180° - (∠ВАЕ + ∠АBD) = 180˚ - (27˚ + 37˚) = 116°

Ответ: 116°