Предмет: Математика,
автор: Аноним
Помогите ,пожалуйста, вычислить интеграл. Нужно полное решение
Приложения:
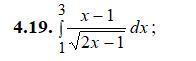
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Первый интеграл:
Второй интеграл решается аналогичной заменой :
Итак,
Вычислим определенный интеграл:
Похожие вопросы
Предмет: Другие предметы,
автор: alena210702
Предмет: Русский язык,
автор: zolotoreva8080
Предмет: Русский язык,
автор: Алина1
Предмет: Математика,
автор: mho1956
Предмет: Литература,
автор: иван971