Предмет: Геометрия,
автор: gamingseries228
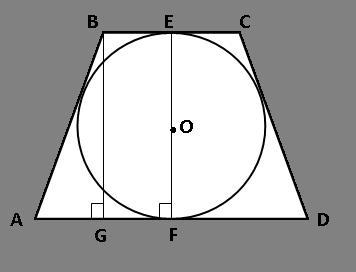
В равнобедренную трапецию вписана окружность. Вычисли боковую сторону трапеции AB и радиус окружности, вписанной в трапецию, если её основания равны 6 см и 12 см.
Приложения:
Ответы
Автор ответа:
33
Ответ:
9 см и 3√ 2
Объяснение:
1. Трапеция равнобедренная, поэтому:
AE= AD−BC2 = (12−6)2 = 3 см.
2. r=0,5 ⋅ BE (т. к. BE равна диаметру окружности, вписанной в трапецию).
trapece 1 - Copy.JPG
3. У трапеции сумма длин противоположных сторон должна быть равна, так как в неё вписана окружность:
AB+CD=BC+AD .
Боковые стороны равны, поэтому 2AB= 6+12 = 18;
AB= 9 см.
4. По теореме Пифагора:
BE= √ AB2−AE2;
BE= √ 92−32 ;
BE= 72−−√2 = √ 2⋅36 ;
BE= 62–√ 2 см;
r=0,5 ⋅ BE= 32–√2 см;
AB= 9 см; r= 32–√2 см.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: санни2003
Предмет: Українська мова,
автор: VikysaSmile
Предмет: Қазақ тiлi,
автор: DamaА
Предмет: Математика,
автор: krutTV43
Предмет: Химия,
автор: kim0001