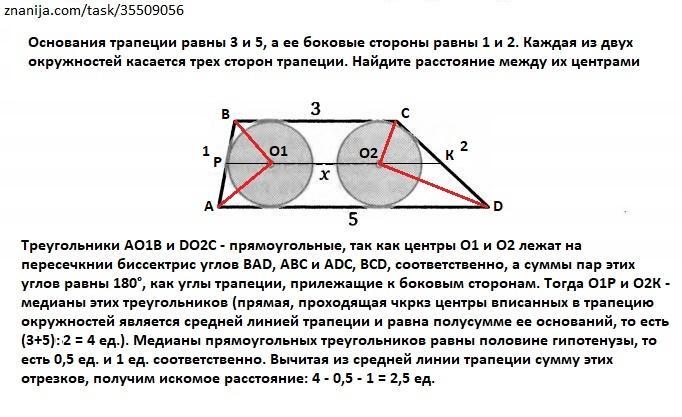
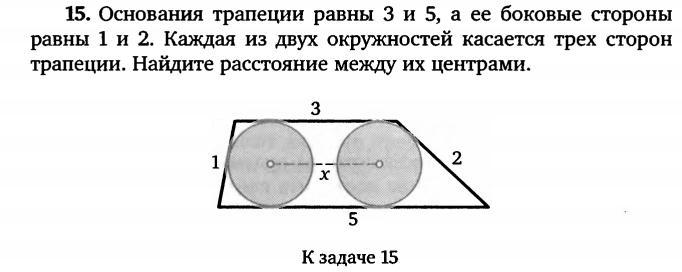
Основания трапеции равны 3 и 5, а ее боковые стороны равны 1 и 2. Каждая из двух окружностей касается трех сторон трапеции. Найдите расстояние между их центрами (рисунок)
Ответы
Ответ:
2,5 ед.
Объяснение:
Пусть О1 и О2 - центры данных окружностей. Соединим вершины трапеции А и В - с О1, C и D - с О2.
Треугольники АО1В и DO2C - прямоугольные, так как центры О1 и О2 лежат на пересечении биссектрис углов BAD, ABC и ADC, BCD, соответственно, а суммы пар этих углов равны 180°, как углы трапеции, прилежащие к боковым сторонам. Тогда О1Р и О2К - медианы этих треугольников (прямая, проходящая через центры вписанных в трапецию окружностей является средней линией трапеции и равна полусумме ее оснований, то есть (3+5):2 = 4 ед.). Медианы прямоугольных треугольников равны половине гипотенузы, то есть 0,5 ед. и 1 ед. соответственно. Вычитая из средней линии трапеции сумму этих отрезков, получим искомое расстояние: 4 - 0,5 - 1 = 2,5 ед.