Предмет: Алгебра,
автор: HopiTakeo
Решить интеграл ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Приложения:
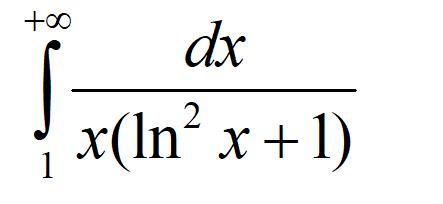
Ответы
Автор ответа:
0
Особые точки:
HopiTakeo:
это точно? в ответе π
продифференцируйте полученную первообразную, получите исходное подлогарифмическое выражение. Двойная подстановка выполнена верно. Так что в ответе своем я уверен
Похожие вопросы
Предмет: Русский язык,
автор: ден4и
Предмет: Русский язык,
автор: nokia8378
Предмет: Русский язык,
автор: SergeiZolot
Предмет: Математика,
автор: inka223
Предмет: История,
автор: kudlan84