Предмет: Геометрия,
автор: Аноним
Прямая касается окружности с центром O в точке B. На касательной по разные стороны от точки B отложены равные отрезки BA и BC. Доказать,что OA = OB.
Приложения:

Hrisula:
В задаче ошибка. ОА не может быть равно ОВ. т.к. ОА - гипотенуза. а ОВ - катет прямоугольного треугольника АОВ. В данном ниже верном решении это учтено.
Ну да ошибка.Учителя спросил он так и ответил.OA=OC,спасибо.
Ответы
Автор ответа:
3
Дано :Окр. О(r)ВС-касательная , А∈ВС, ВА=ВС.
Доказать :OA = OС
Объяснение:
Касательная , проведенная в точку касания, перпендикулярна радиусу ⇒∠АВО=∠СВО=90°
ΔАВО=ΔСВО как прямоугольные по двум катетам : АВ=СВ по условию, ВО-общая. В равных треугольниках соответственные элементы равны , значит ОА=ОС.
Приложения:
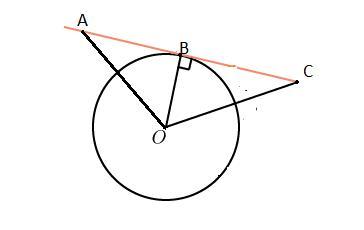
Но смотрите,тут нужно показать что AO = OB,а по вашему объявлению AO = CO,не верно если так подумать
Ток в условии AC касательная.
Похожие вопросы
Предмет: Английский язык,
автор: Ancapitonowa
Предмет: Русский язык,
автор: diano4ka2004
Предмет: Русский язык,
автор: Funny2517
Предмет: География,
автор: Реджина40
Предмет: Математика,
автор: Лолаложка