Предмет: Математика,
автор: natabaranova06
В двух бочках вместе 1020 л бензина. Когда из первой бочки взяли 2/5 бензина, а из второй бочки взяли 1/7 бензина, то в обеих бочках бензина стало поровну. Сколько литров бензина было в каждой бочке первоначально?
Ответы
Автор ответа:
0
Ответ:
420 600
Пошаговое объяснение:
Приложения:
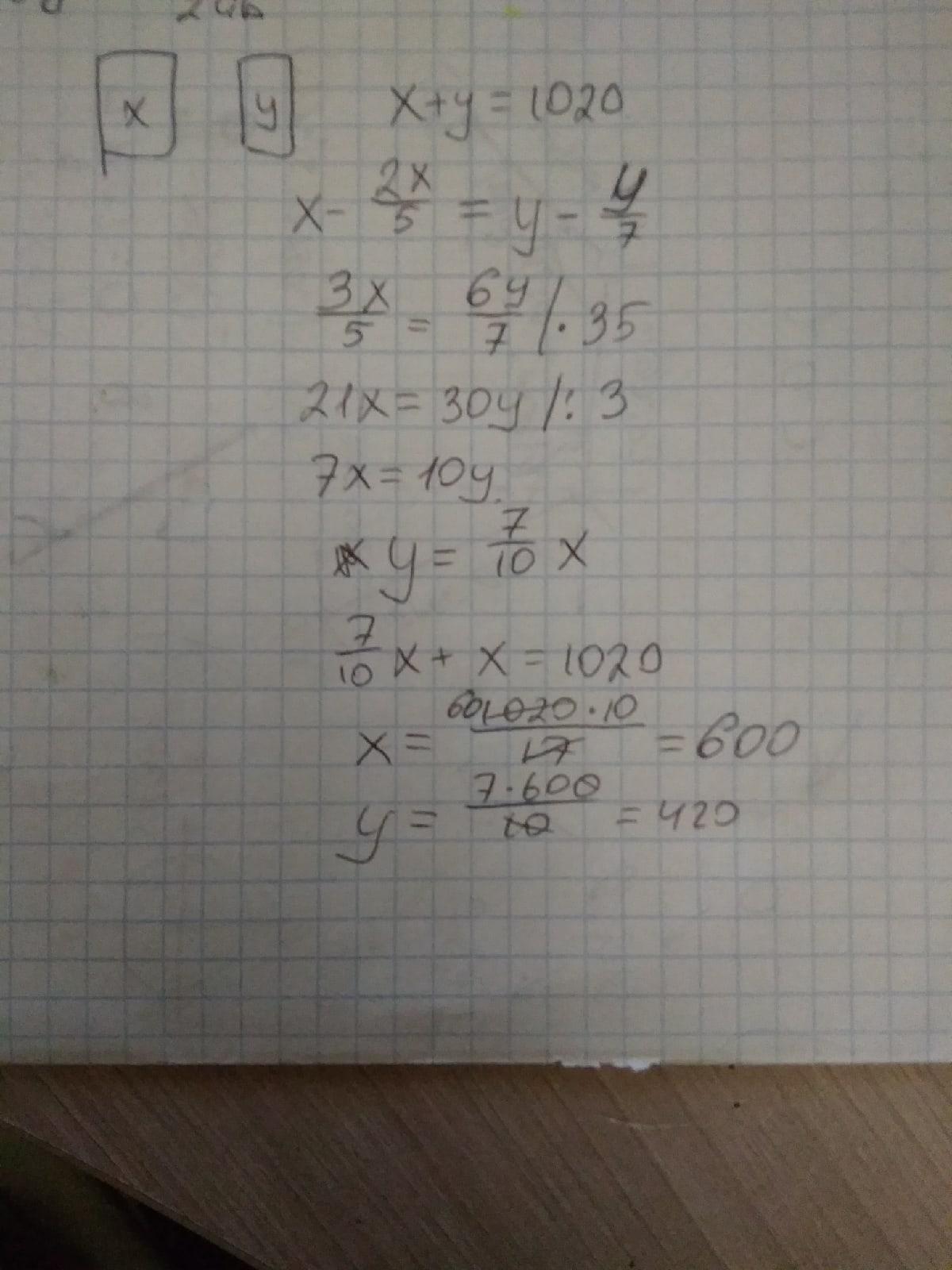
Автор ответа:
0
Ответ: 600 л и 420 л.
Пошаговое объяснение:
Пусть х л было в первой бочке, тогда (1020-х) л - было во второй бочке;
(1-2/5)х л=3/5 х л - стало в первой бочке,
(1-1/7)*(1020-х) л= 6/7*(1020-х) л - стало во второй бочке.
По условию задачи в бочках стало поровну.
Составим и решим уравнение:
3/5 х = 6/7* (1020-х);
3/5 х = 6/7*1020 - 6/7 х;
3/5 х + 6/7 х = 6120/7;
Умножим обе части уравнения на 35, одновременно сокращая этот множитель со знаменателями:
21 х +30 х= 30600;
51 х=30600;
х=30600:51;
х=600.
1020-х=1020-600=420.
Похожие вопросы
Предмет: Русский язык,
автор: OlgaKyznecova
Предмет: Русский язык,
автор: fatima
Предмет: Русский язык,
автор: Дашулямерзликина
Предмет: Литература,
автор: sidjeimer
Предмет: Химия,
автор: поже13