Question

Знайдіть площу основи правильної чотирикутної піраміди, висота якої становить корінь з 2, якщо її бічне ребро дорівнює корінь з 3
Бажано з малюнком

Answer 1

Ответ:

Площадь основания равна 2 ед².

Объяснение:

Найдите площадь основания правильной четырехугольной пирамиды, высота которой равна √2, если ее боковое ребро равно √3.

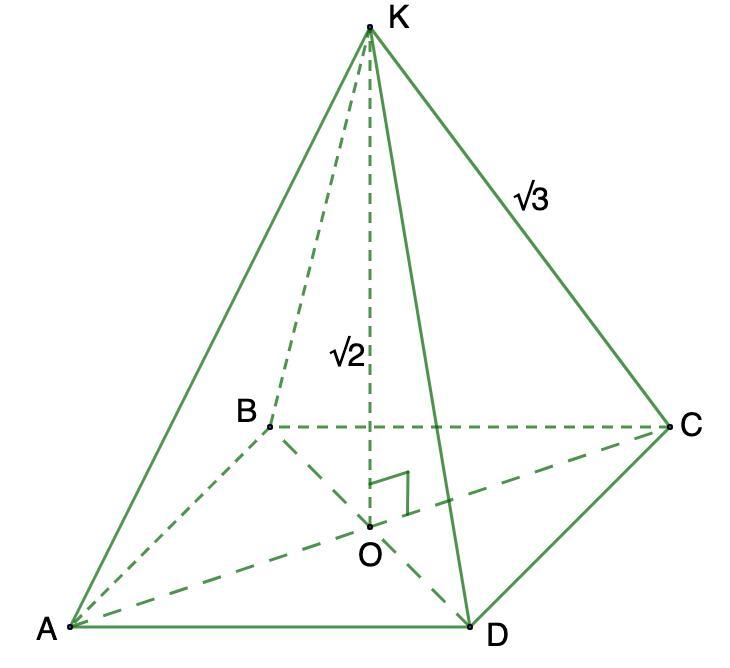
Дано: KABCD - правильная пирамида;

КО = √2 - высота;

КС = √3 - боковое ребро.

Найти: S(ABCD)

Решение:

• В основании правильной четырехугольной пирамиды лежит квадрат.

Значит, нам нужно найти площадь квадрата:

S = a², где а - сторона квадрата.

⇒ ищем сторону квадрата АВСD.

1. Рассмотрим ΔОКС - прямоугольный.

По теореме Пифагора найдем ОС:

ОС² = КС² - КО² = 3 - 2 = 1

ОС = √1 = 1

2. Рассмотрим ΔВОС.

• Диагонали квадрата равны.

⇒ АС = DB

• Диагонали квадрата точкой пересечения делятся пополам.

⇒ ВО = ОС = 1

• Диагонали квадрата взаимно перпендикулярны.

⇒ АС ⊥ DB.

Делаем вывод: ΔВОС - прямоугольный, равнобедренный.

По теореме Пифагора найдем ВС:

ВС² = ОВ² + ОС² = 1 + 1 = 2

ВС = √2

Сторону квадрата знаем, можем найти площадь:

S(ABCD) = BC² = 2

Площадь основания равна 2 ед².

#SPJ5