Срочно, пожалуйста нужна помощь!!!
Ответы
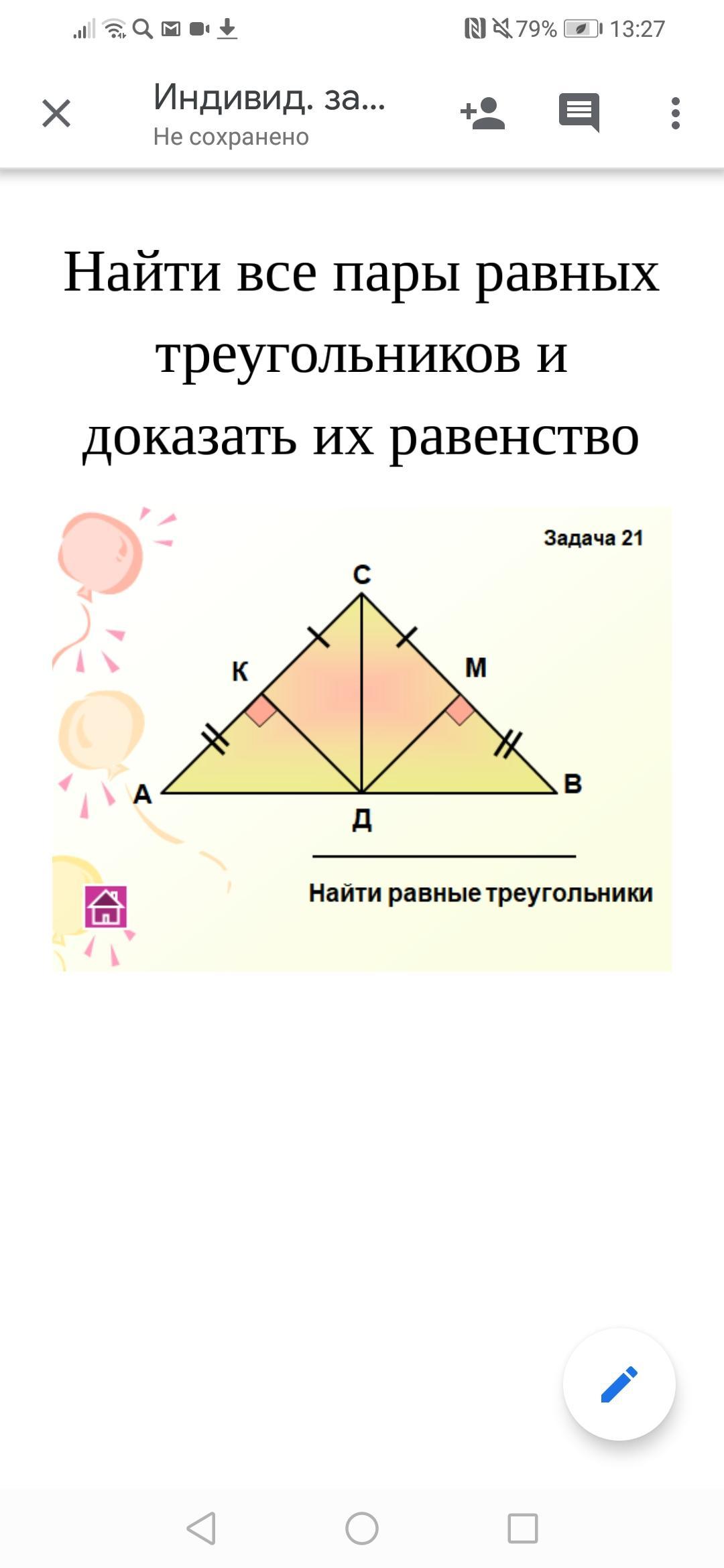
На треугольнике АВС отмечены: на стороне АС - точка К, на стороне ВС - точка М так, что АК=ВМ, КС=МС. На основании АВ - точка Д. Отрезок ДК⊥АС, отрезок ДМ⊥ВС, Найти все пары равных треугольников и доказать их равенство. (см. рисунок в задании).
Ответ: а) ∆КСД=∆МСД б) ∆ АКД=∆ ВМД ; в) ∆ АСД=∆ ВСД
Объяснение:
а) Треугольники КСД и МСД прямоугольные. Катеты КС=МС, гипотенуза СД - общая. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны =>
∆ КСД=∆МСД.
б) Из доказанного выше КД=МД. По условию АК=МВ=> прямоугольные ∆ АКД=∆ ВМД по двум катетам.
в) В ∆ АСД и ∆ ВСД стороны АС=ВС ( состоят из равных частей), АД=ВД ( из п.б) и СД - общая. => ∆ АСД=∆ ВСД по трем сторонам.