Question

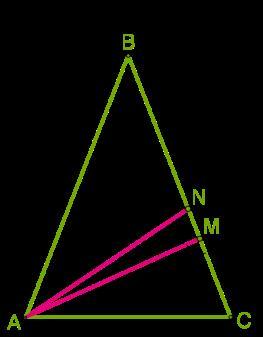
В равнобедренном треугольнике к боковой стороне проведена высота и биссектриса угла, прилежащего к основанию.

Определи угол между высотой и биссектрисой, если угол вершины ∡ B = 38°.

∡ MAN=

Answer 1

Ответ:

∡ МАN = 16,5°

Объяснение:

1) если треугольник АВС равнобедренныц, значит углы при основании равны, т.е. угол А = углу С = (180 - 38 ) ÷ 2 = 142 ÷ 2 = 71°

2) треугольник АМВ прямоугольный, т.к. АМ высота в треугольнике АВС, значит

∡ ВАМ = 180 - 90 - 38 = 52°

3) ∡ BАN = ∡ САN =71 ÷ 2 = 35,5° , т.к. АN биссектриса ∡ ВАС

4) ∡ МАN = ∡ ВАМ - ∡ ВАN = 52 - 35,5 = 16,5°