Предмет: Геометрия,
автор: englishmusicperm
Нарисуй прямоугольный треугольник ABC так, чтобы ∢C =90°,
CA= 9 см и CB= 12 см.
Вычисли BA=
см и напиши отношение CA:BA =
:
(дробь не сокращай).
Приложения:
Ответы
Автор ответа:
4
Ответ:
Объяснение:
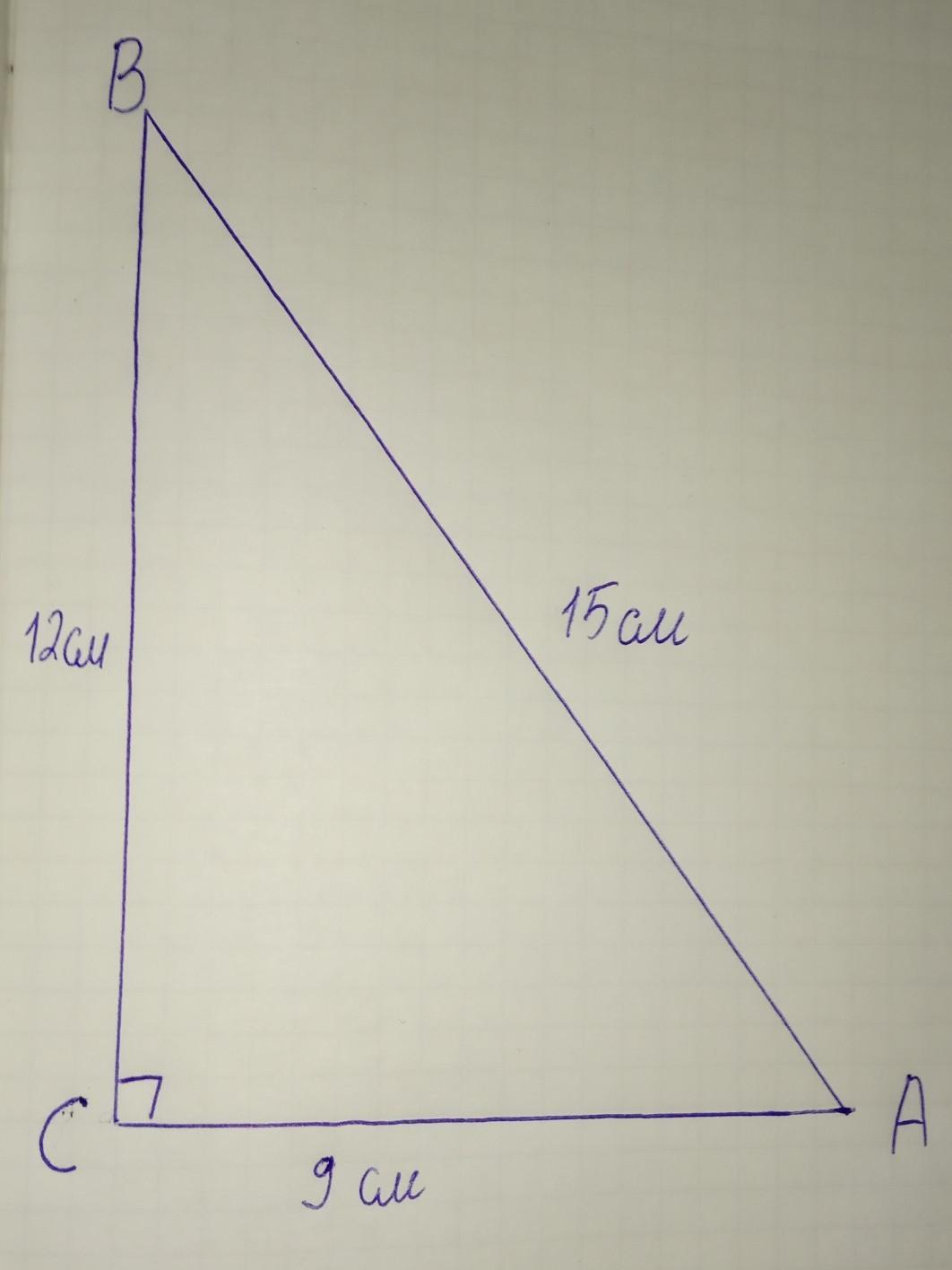
Начертим прямоугольный треугольник ABC так, чтобы ∢C =90°, СА = 9 см и CB = 12 см.
Если ∢C = 90°, тогда СА и СВ будут катетами этого треугольника, а ВА - гипотенуза.
Найдём гипотенузу, используя т. Пифагора:
c² = a²+b² => c = √(a²+b²)
В данном случае:
ВА = √(СА²+СВ²) = √(9²+12²) = √(81+144) = √225 = 15 см.
Теперь, зная все стороны этого треугольника, найдём отношение наименьшей стороны данного треугольника (катета СА) и наибольшей стороны (гипотенузы ВА), при этом в вычислениях дробь НЕ будем сокращать:
АС/ВА = 9/15
Рисунок дан во вложении.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: yavanyaas
Предмет: Русский язык,
автор: лёля101
Предмет: Русский язык,
автор: KatyaBelka
Предмет: Математика,
автор: Сергейчук1
Предмет: История,
автор: alinocka13