Помогите пожалуйста!)
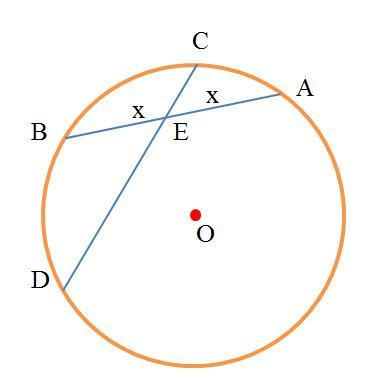
Из двух пересекающихся хорд одна разделилась на части в 36 см и 9 см, а другая - пополам. Найдите длину второй хорды.
Ответы
Ответ:
a) Введём обозначения (см. рисунок). По теореме о пересекающийся хорд
AE•EB=CE•ED или x²=CE•ED.
Подставим известные значения и находим x:
x²=CE•ED=9•36=3²•6²
x=3•6=18 см.
Находим длину второй хорды
AB=2•x=2•18=36 см.
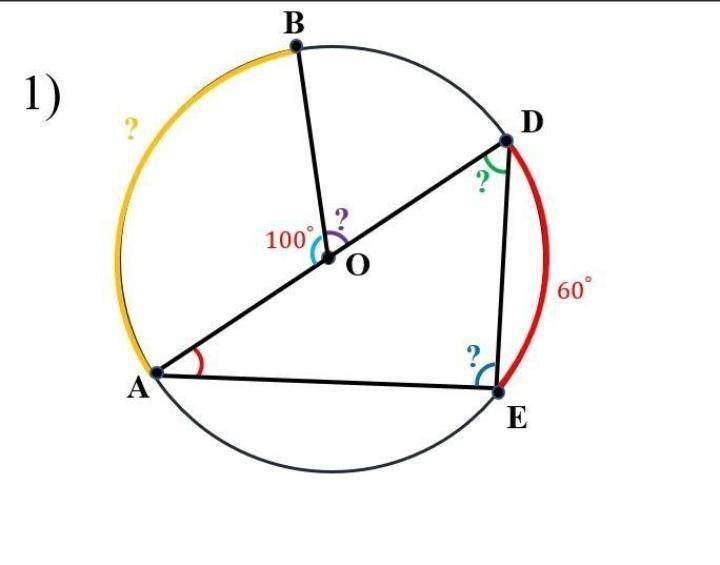
1) Градусная мера дуги BA равна центральному углу BOA и поэтому равна 100°, то есть дуга BА=100°.
Так как угол AOD развёрнутый и равен 180°, то угол определяем как смежный угол с углом BOA:
∠BOD=180°–∠BOA=180°–100°=80°.
Как было отмечено, центральный угол AOD развёрнутый и равен 180°. Тогда градусная мера дуги DBA равна 180°. Далее, ∠AED вписанный, то по свойству вписанного угла, измеряется половиной дуги DBA, на которую опирается. Отсюда
∠AED=180°:2=90°
(для нахождения угла AED можно было использовать свойство вписанного угла, которая опирается на диаметр).
Угол DAE вписанный, то по свойству вписанного угла, измеряется половиной дуги ED, на которую опирается. Так как градусная мера дуги ED равна 60°, то ∠DAE=60°:2=30°. Известно, что сумма всех внутренних углов треугольника ADE равна 180°. Поэтому
∠АDE= 180°–∠AED –∠DAE=180°–90° –30°=60°.