Предмет: Геометрия,
автор: yulyarozenberg
УМОЛЯЯЯЮ, ПОМОГИИТЕ, ПОСЛЕДНЯЯ НАДЕЖДА НА ВАС, БЫЛА БЫ БЕЗУУУМНО БЛАГОДАРНА, ПРАВДА. эта задача на оценку, с решебн нельзя, сама не очень понимаю. Из точки М биссектрисы неразвернутого угла О проведены перпендикуляры МА и MB к сторонам этого угла. Докажите, что AB⊥OM и нарисуйте рисунок к задаче.
Ответы
Автор ответа:
10
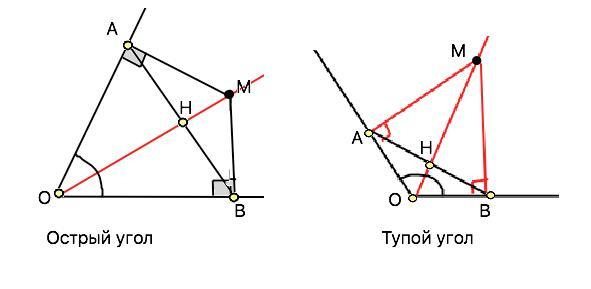
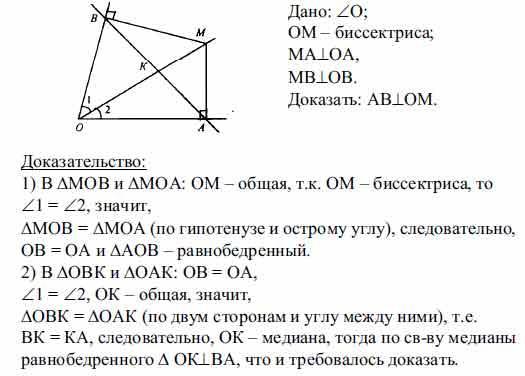
Доказательство для острого и тупого угла одинаково.
По условию ОМ - биссектриса, МА⊥ОА, МВ⊥ОВ =>
Треугольники АОМ и ВОМ прямоугольные, имеют общую гипотенузу ОМ и по равному острому углу ( ∠АОМ=∠ВОМ).
∆ АОМ=∆ ВОМ по 3-му признаку равенства прямоугольных треугольников. . Следовательно, их катеты АО=ВО, поэтому ∆ АОВ - равнобедренный .
В равнобедренном треугольнике биссектриса угла между равными сторонами - еще и медиана и высота.
Высота ОН⊥АВ, ОН принадлежит ОМ. ⇒
АВ⊥ОМ, ч.т.д.
Приложения:
yulyarozenberg:
больше спасибо!
кто химию хорошо знаеь зайдите в профиль посмотрите
вопрос
Автор ответа:
8
Ответ:вот
Объяснение:
Приложения:
зачем ты скинул решение из других источников? я же написала, что с других источников нельзя.
не знаю брат
Похожие вопросы
Предмет: Английский язык,
автор: pro100serj
Предмет: Другие предметы,
автор: gtagta11
Предмет: Русский язык,
автор: erohingermanгерман
Предмет: Математика,
автор: Palinka1
Предмет: Математика,
автор: АринаГеровская2002