Question

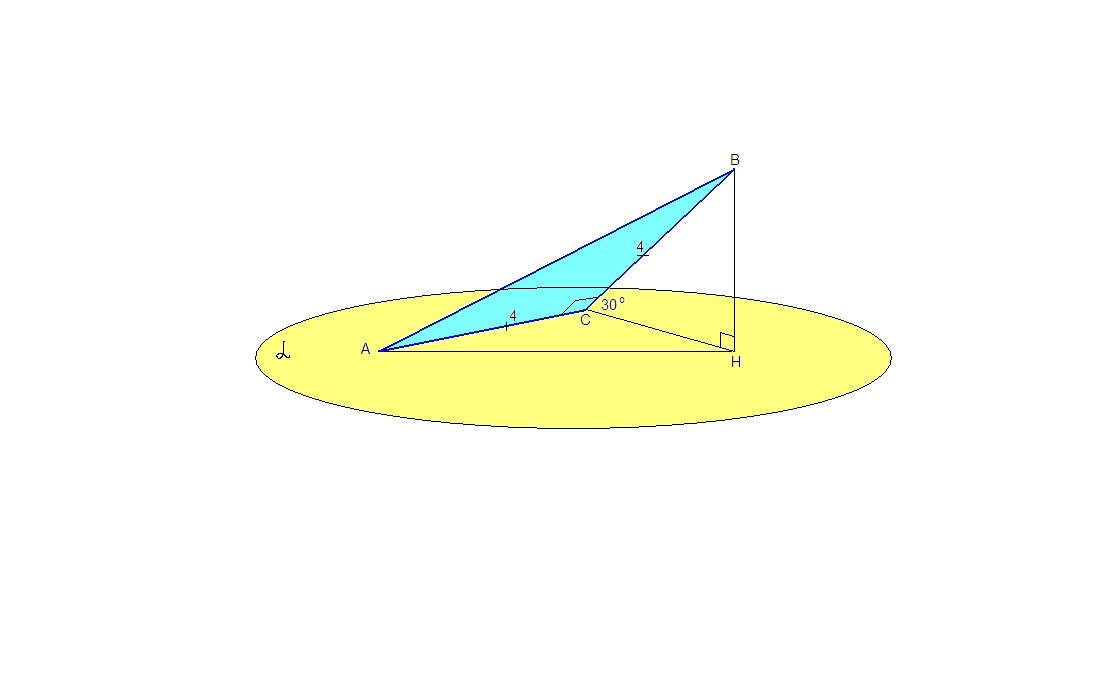
Длина катета прямоугольного равнобедреного треугольника равна 4 см, плоскость α проходящая через катет,образует с плоскостью тругольника угол,величина которого равна 30 градусов.Найдите длину проэкции гипотенузы на плоскость.

Answer 1

Проведем ВН⊥α.
Тогда АН - проекция гипотенузы АВ на плоскость α.
АН - искомая величина.

ВС⊥АС как катеты прямоугольного треугольника,
НС - проекция ВС на плоскость α, значит
НС⊥АС по теореме, обратной теореме о трех перпендикулярах.
∠ВСН = 30° - линейный угол двугранного угла между плоскостью треугольника и плоскостью α.

ΔВСН: ∠ВНС = 90°, ВН = ВС/2 = 4/2 = 2 см как катет, лежащий напротив угла в 30°.

ΔАВС: ∠АСВ = 90°, по теореме Пифагора
             АВ = √(АС² + ВС²) = √(4² + 4²) = 4√2 см

ΔВНА: ∠ВНА = 90°, по теореме Пифагора
             АН = √(АВ² - ВН²) = √(32 - 4) = √28 = 4√7 см