Предмет: Геометрия,
автор: kirilg93
У ромбі більша діагональ поділяє висоту на відрізки 3 і 5 см. Знайти косинус тупого кута
Ответы
Автор ответа:
1
Ответ:
Объяснение:
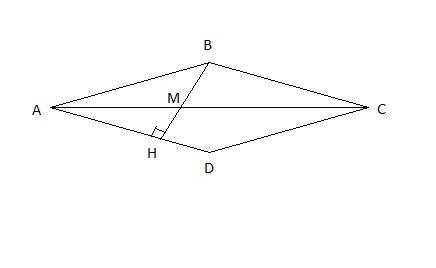
MH = 3, BM = 5
ΔΔAMH и MBC прямоугольные, т.к. BH - высота.
∠AMH = ∠BMC (как вертикальные)
⇒ ΔAMH подобен ΔMBC (по двум углам)
Из подобия треугольников:
Т.к. в ромбе AB = BC, то аналогично
Требуемый тупой угол ∠ABC = ∠ABH + ∠HBC = ∠ABH + 90°
Окончательно получаем:
cos(∠ABC) = cos(∠ABH + 90°) = - sin(∠ABH) =
(Синус находим из прямоугольного ΔABH)/
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: anutka0611
Предмет: Английский язык,
автор: mitina2000
Предмет: Русский язык,
автор: Котэшка55
Предмет: Математика,
автор: forosheekonata
Предмет: Математика,
автор: Рапунцель111111