Question

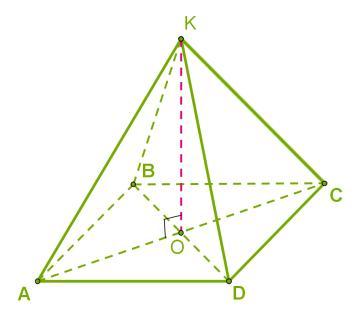
Дана правильная четырёхугольная пирамида, все рёбра которой равны 18 см.
Определи объём данной пирамиды.

Answer 1

Объем правильной четырехугольной пирамиды равен одной трети произведения площади квадрата, являющегося основанием S (ABCD) на высоту h (KO).  

    $V=\frac{1}{3}S_o \cdot h \\\\V=\frac{1}{3}S_{ABCD}\cdot KO$

Найдем площадь основания:

    $S \boxed {} = a^2\\S_{ABCD} = AB^2\\S_{ABCD} = 18^2 = 324 \:\: (cm^2)$

Найдем катет AO треугольника AOK:

    $AO=\frac{1}{2}AC \\AC = \sqrt{18^2+18^2} = \sqrt{18^2(1+1})=\sqrt{18^2}\sqrt{2} =18 \sqrt{2} \:\: (cm)\\AO=\frac{1}{2}AC =\frac{18 \sqrt{2}}{2} = 9\sqrt{2} \:\: (cm)$

Найдем катет KO (h) треугольника AOK:

    $KO=\sqrt{18^2-\left(9\sqrt{2}\right)^2} =\sqrt{324-162}= \sqrt{162} =\sqrt{81}\sqrt{2} =9\sqrt{2} \:\: (cm)$

Подставим значения в формулу объема правильной четырехугольной пирамиды:

    $V=\frac{324}{3} \cdot 9\sqrt{2} =108\cdot 9\sqrt{2}=972\sqrt{2} \:\: (cm^3)$

Ответ: Объем пирамиды равен 972√2 cm³.