Предмет: Алгебра,
автор: AnastasiiaMoonlight
А что делать со вторым условием?
Подскажите пожалуйста, буду очень признательна
Приложения:
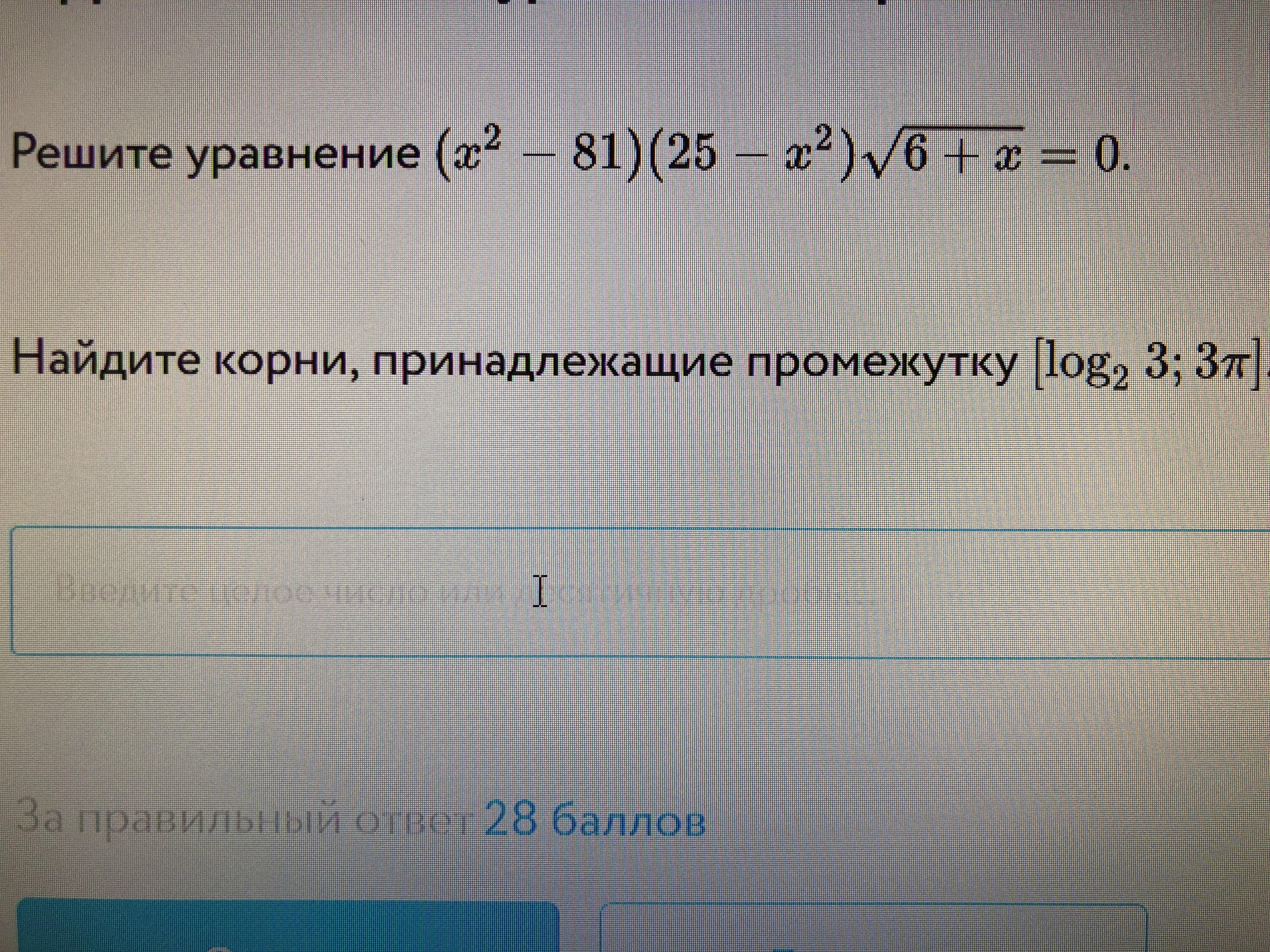
Ответы
Автор ответа:
0
Ответ:
5 и 9
Объяснение:
Корни уравнения: 9; -5; 5; -6
(-9 не подходит, так как под корнем будет отрицательное число!)
У нас должно выполниться двойное неравенство:
log₂3≤x≤3π, где x - наш корень
наибольший из корней: 9
сравним его с 3π:
так как 3π≈3*3.14=9.42, то
9<3π - значит и все другие корни меньше чем 3π.
Но при этом каждый из корней должен быть больше log₂3
1 способ (универсальный)
сравниваем числа:
Аналогично проверяем 9
Проверяем оставшиеся числа и выясняем, что подходят только 5 и 9
2 способ (для данного примера)
так как log₂2=1 и log₂4=2, значит 1<log₂3<2.
Получается, что только числа 5 и 9 будут больше чем log₂3
Похожие вопросы
Предмет: Английский язык,
автор: Boo000
Предмет: Русский язык,
автор: cat1111
Предмет: Русский язык,
автор: rita04011986
Предмет: Математика,
автор: loveket
Предмет: Алгебра,
автор: penapllepen