Question

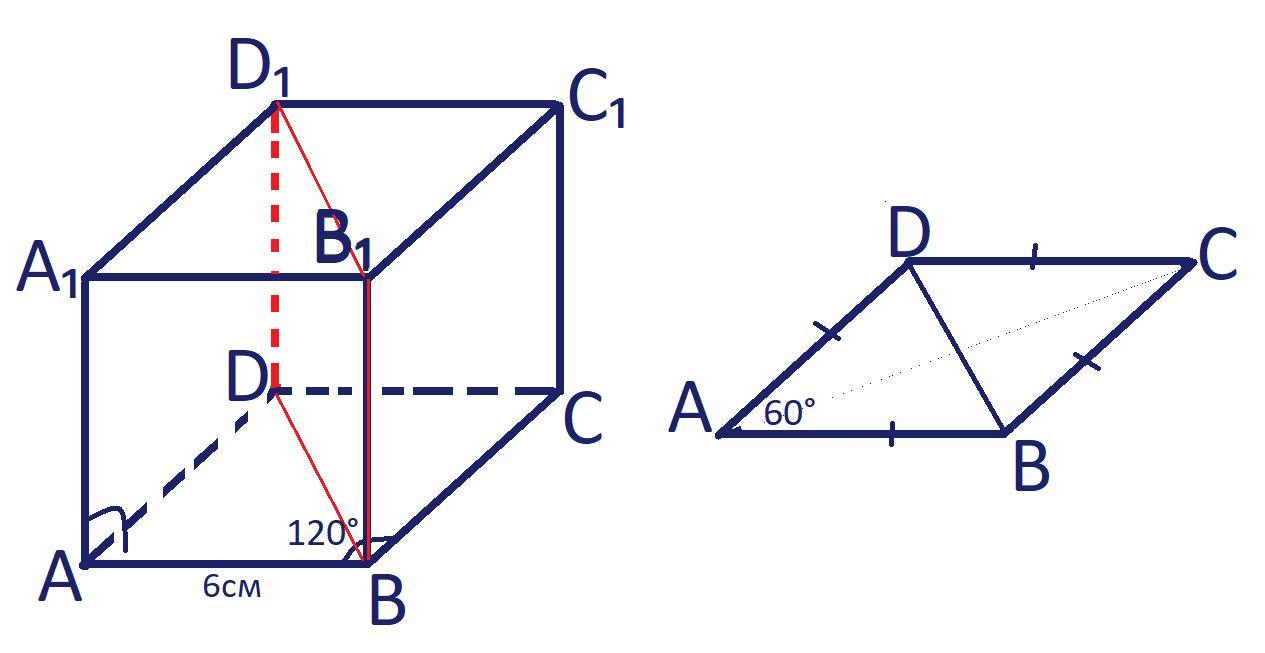
Помогите с геометрией срочно!!! У прямой четырёхугольной призмы в основании лежит ромб с углом 120° и стороной 6 см. Определи площадь меньшего диагонального сечения, если высота призмы — 2 см.

Answer 1

Пусть дана прямая призма ABCDA₁B₁C₁D₁, при этом ABCD - основание,  

∠ABC=120°, AB = 6см, H = 2см.  

• Сумма соседних углов ромба равна 180°.

В ромбе ABCD:

∠B+∠A = 180°;

∠A = 180°-∠B;

∠A = 180°-120° = 60°;

• Против меньшего угла ромба лежит меньшая диагональ.

∠A < ∠B  ⇒  BD < AC;

• Все стороны ромба равны между собой.

AB = AD = 6см.

По теореме косинусов в △ABD:

BD² = AB²+AD²-2·AB·AD·cos∠A;

BD² = 2·AB²-2AB²·cos60° =  2·AB²-2AB²·(1/2);

BD² = 2AB²-AB² = AB²;

BD = AB = 6см.

• Все боковые рёбра прямой призмы равны её высоте и перпендикулярны основанию. Поэтому меньшее диагональной сечение проходит через меньшею диагональ сечения.

DD₁ = BB₁ = H = 2см;

BB₁║DD₁ т.к. BB₁⊥(ABC)  и  DD₁⊥(ABC);

BB₁⊥(ABC),  BD⊂(ABC)  ⇒  BB₁⊥BD.

BB₁D₁D - прямоугольник т.к. (BB₁║DD₁; DD₁ = BB₁; BB₁⊥BD),

• Площадь прямоугольника равна произведению смежных сторон.

S(BB₁D₁D) = BB₁·BD = 2см·6см = 12 см².

Ответ: 12см².