Question

Из точки, взятой вне плоскости, проведены две наклонные к этой плоскости , длины которых 10 см и 7 см. Проекции этих наклонных на плоскость относятся, как 6:√15. Определить расстояние от этой точки до плоскости.

Answer 1

Ответ:

(2√154)/7 см

Пошаговое объяснение:

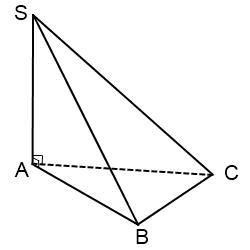
SC=10 см, SB=7 см, AC:AB=6:√15

AC=6k см; AB=√15k см

SA⊥ABC⇒SA⊥AB; SA⊥AC⇒∠SAB=∠SAC=90°

По теореме Пифагора:

SA²=SC²-AC²=10²-(6k)²=100-36k²

SA²=SB²-AB²=7²-(√15k)²=49-15k²

SB²-AB²=SC²-AC²⇒100-36k²=49-15k²

21k²=51

k²=51/21=17/7

SA²=100-36k²=100-36·(17/7)=88/7

SA=√(88/7)=(2√154)/7