Предмет: Алгебра,
автор: hhhgss
знайдіть площу фігури, обмеженої графіком функції f(x), графіком дотичної до нього в точці х0=1 та прямою х=0
f(x) = x^2-4x
sangers1959:
Графік функції f(x) чему равен?
Ответы
Автор ответа:
2
Ответ: S=1/3 кв. ед.
Объяснение:
f(x)=x²-4x x₀=1 x=0 S=?
yk=y(x₀)+y'(x₀)*(x-x₀)
y(1)=1²-4*1=1-4=-3.
y'(1)=(x²-4x)'=2x-4=2*1-4=2-4=-2. ⇒
yk=-3-2*(x-1)=-3-2x+2=-2x-1.
y=x²-4x y=-2x-1 x=0 S=?
x²-4x=-2x-1
x²-2x+1=0
(x-1)²=0
x-1=0
x=1. ⇒
S=₀∫¹(x²-4x-(-2x-1)dx=₀∫¹(x²-4x+2x+1)dx=₀∫¹(x²-2x+1)dx=
=₀∫¹x²dx-₀∫¹2xdx+₀∫¹dx=(x³/3-x²+x) ₀|¹=(1³/3)-1²+1-(0³/3-0²+0)=1/3.
Приложения:
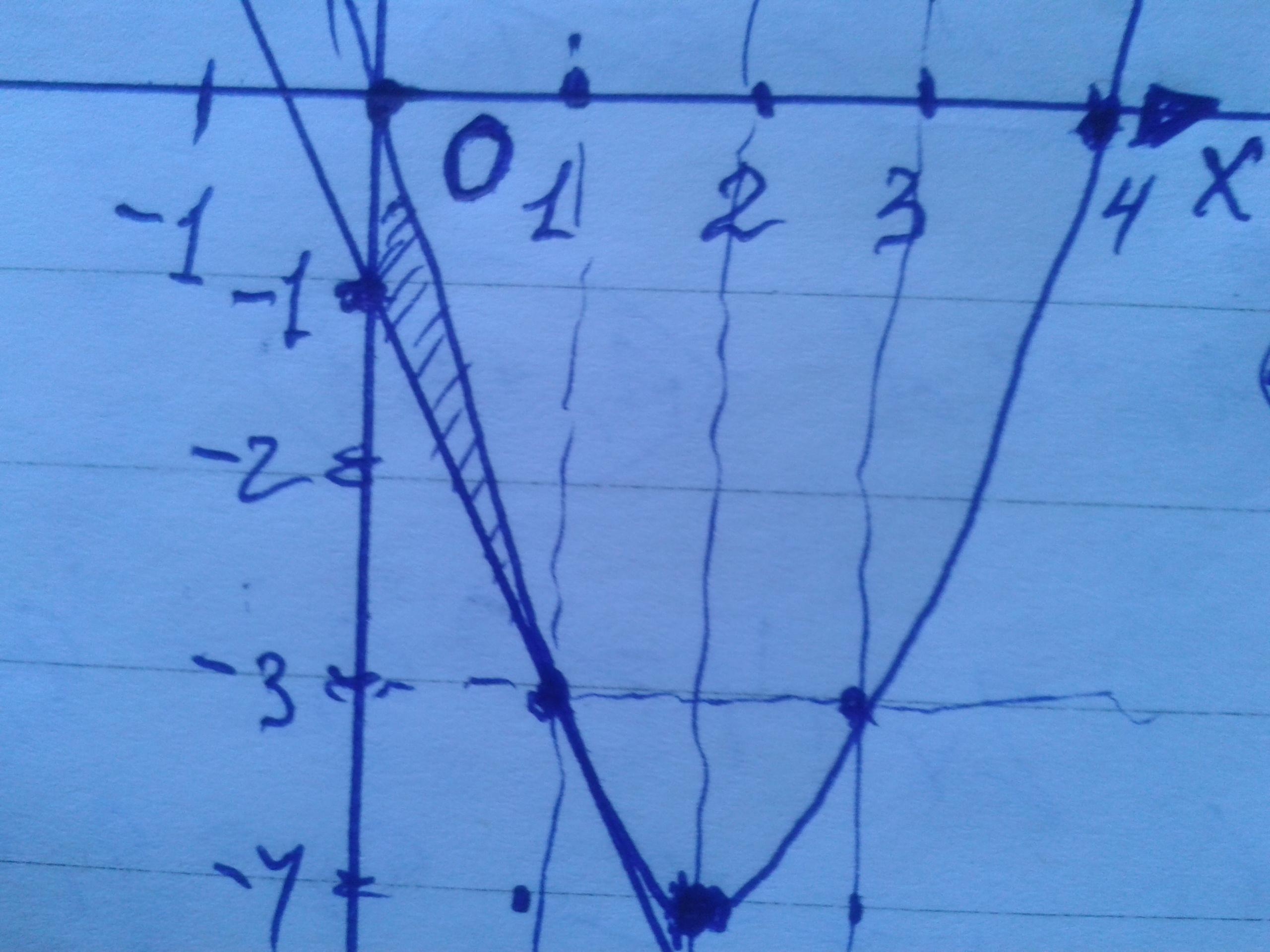
Похожие вопросы
Предмет: Русский язык,
автор: тывапы2000
Предмет: Английский язык,
автор: Александра2902
Предмет: Українська мова,
автор: slav73
Предмет: Математика,
автор: mamazzz