Предмет: Геометрия,
автор: evaredkina291
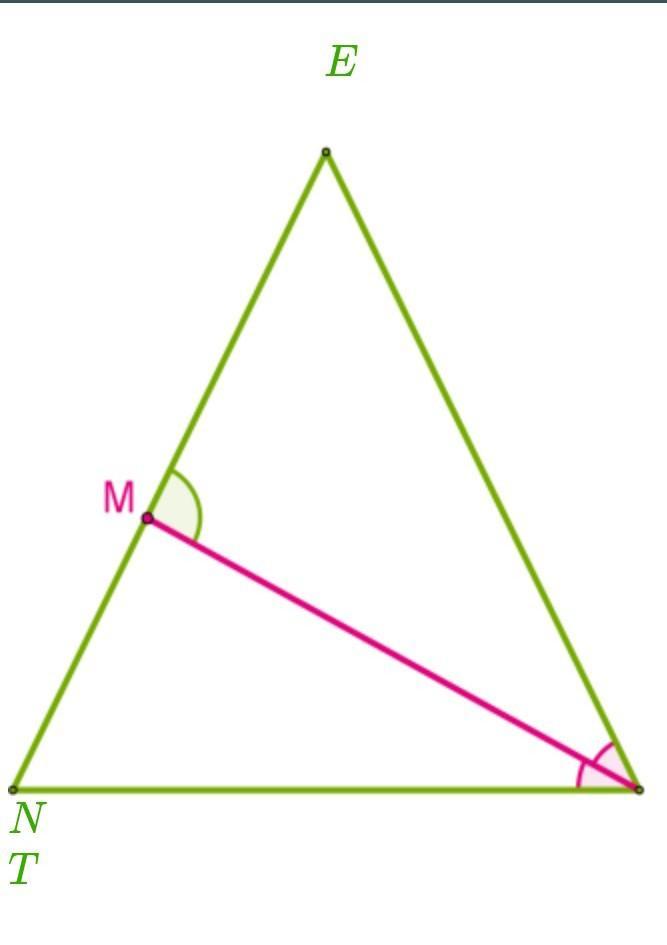
В равнобедренном треугольнике NET проведена биссектриса TM угла T у основания NT,
∡ TME = 78°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).
∡ N = °;
∡ T = °;
∡ E = °.
Приложения:
Ответы
Автор ответа:
12
Объяснение:
Если угол ТМЕ=78 градусам, то смежный ему угол ТМN=180-78=102 градусам.
Рассмотрим теперь треугольник ТМN. Сумма его углов равна 180 градусам. Угол ТМN мы вычислили. Известно также, что угол N вдвое больше угла NTM (углы N и Т равны, поскольку треугольник NET - равнобедренный, а угол NTM равен половине угла N или угла Т, т. к. TM - биссектриса угла Т).
Получаем: N + TMN + NTM = 180
N + 102 + 0,5*N = 180
1,5N = 180-102
1,5N = 78
N = 52 градусов
Раз угол N = 52, то угол Т также равен 52 градусам. Угол Е = 180 - 52 - 52 = 180-104=76 градусам.
вроде так
evaredkina291:
да, это правильно, спасибо
Похожие вопросы
Предмет: Русский язык,
автор: 1236546
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Slimi
Предмет: Алгебра,
автор: Arinatum1