Предмет: Геометрия,
автор: polina2005io1113
ПОМОГИТЕ ПОЖАЛУЙСТА ДАМ МНОГО БАЛЛОВ ЗАРАНЕЕ СПАСИБО!!!!
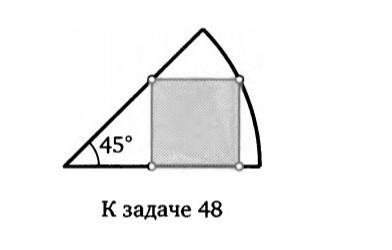
В сектор круга радиуса 1 с углом 45° вписан квадрат, так что
одна его вершина лежит на окружности. Найдите площадь квадрата.
Приложения:
Ответы
Автор ответа:
14
Ответ:
0,2
Объяснение:
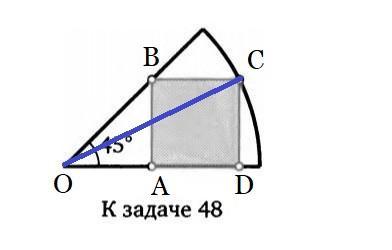
ΔOAB - прямоугольный, <BOA = 45°, ⇒ <ABO = 90° - 45° = 45°, ⇒ ΔOAB - равнобедренный, ⇒ OA = OB.
Пусть AB = x, тогда AD = x = CD, т.к. ABCD - квадрат.
Построим отрезок OC, OC - радиус по построению, т.к. О - центр окружности, а точка C лежит на окружности, ⇒ OC = 1.
Рассмотрим прямоугольный ΔODC: OD = OA + AD = x + x = 2x, CD = x, тогда по теореме Пифагора OC² = OD² + CD² , получаем уравнение:
1² = (2x)² + x²
1 = 4x² + x²
5x² = 1
x² = 1/5 = 0,2
- сторона квадрата, тогда площадь квадрата x² = 0,2
Приложения:
polina2005io1113:
спасибо большое
Пожалуйста)
Похожие вопросы
Предмет: Русский язык,
автор: Veta25
Предмет: Английский язык,
автор: Kriska1
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: kER11111