Предмет: Математика,
автор: Аноним
Высшая математика. Задание: Вычислить объем фигуры ограниченной линиями.
Нужно полное решение
Приложения:
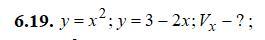
Ответы
Автор ответа:
0
Найдём пересечение функций:
Получили пределы интегрирования -3 и 1. Находим объем по формуле:
Похожие вопросы
Предмет: Русский язык,
автор: Аннагалстян11
Предмет: Русский язык,
автор: 55768
Предмет: Қазақ тiлi,
автор: Raim1401
Предмет: Биология,
автор: Flaman
Предмет: История,
автор: 2000алексей