Предмет: Геометрия,
автор: SuicideMalkov
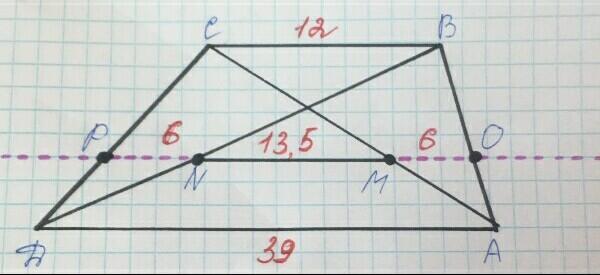
M и N — серединные точки диагоналей AC и BD трапеции ABCD. Определи длину отрезка MN, если длины оснований трапеции AD= 39 см и BC= 12 см.
Ответы
Автор ответа:
12
Решение:
Проведём от точки N к точке P отрезок PN и от точки M к точке O отрезок MO так, что MN - часть средней линии данной трапеции. Соответственно, исходя из этого условия и зная длины BC и AD найдём длину отрезка PO.
(см).
Вернёмся к условию задачи. M и N — СЕРЕДИННЫЕ точки диагоналей AC и BD трапеции ABCD. И следовательно из ранее сказанной записи "MN - часть средней линии данной трапеции" мы можем сказать, что PN и MO равны сумме BC.
(см).
Поскольку нам известен отрезок, на котором находится искомый отрезок MN и два составляющих по бокам отрезка PO, то найдём отрезок MN.
(см)
Ответ:  (см).
(см).
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: mark9
Предмет: Русский язык,
автор: Александра7777
Предмет: Другие предметы,
автор: DIANA2801
Предмет: Экономика,
автор: abiersack