Предмет: Математика,
автор: S01K
Запишите комплексные числа в алгебраической, тригонометрической и пока-зательной формах
Приложения:
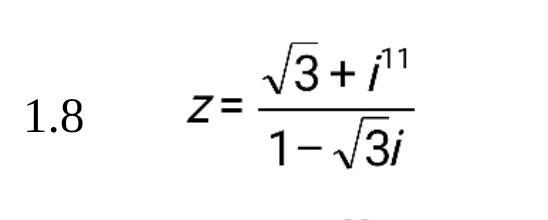
Ответы
Автор ответа:
1
Алгебраическая форма записи:
Тригонометрическая форма записи:
Зная, что и
найдем аргумент:
.
Тригонометрическая форма записи:
Показательная форма записи:
Показательная форма записи:
Похожие вопросы
Предмет: Українська мова,
автор: SofiaF123
Предмет: Русский язык,
автор: Lex200
Предмет: Русский язык,
автор: Aily
Предмет: Математика,
автор: Юлечка363825