Помогите пожалуйста с геометрией.
Ответы
Объяснение:
1)
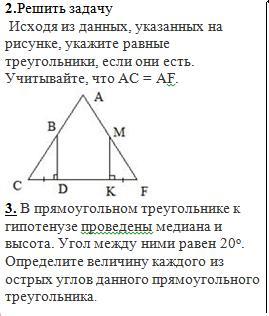
Дано ΔCAF ,CA=AF ,CD=KF, BD⊥CF ,MK⊥ CF.
Доказать ΔCBD= ΔFMK.
Доказательство.
BD⊥CF , MK⊥ CF ⇒ ∠BDC=90°, ∠MKF=90° .
Т.к. CA=AF ,то ΔCAF –равнобедренный и ∠С=∠F .
Тогда ΔCBD= ΔFMK как прямоугольные по катету и прилежащему острому углу: катеты CD=KF по условию, ∠С=∠F ( см. выше).
2)
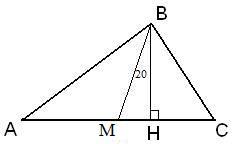
Дано ΔАВС , ∠С=90° , медиана СМ , высота СН, ∠МСН=20°
Найти ∠А, ∠В
Решение.
ΔАВС , ∠С=90° , BМ- медиана значит М- является центром описанной окружности вокруг ΔАВС. Следовательно, AМ=МC=МB
ΔСМН-прямоугольный, ∠СМН=90°-20°=70° по св. острых углов прямоугольного треугольника.
Угол ∠СМН является внешним для ΔАСМ.
ΔАСМ– равнобедренный со сторонами AМ=МС, значит углы при основании AС равны. Тогда ∠САМ=∠АСМ=70°:2=35° , по т. о внешнем угле.
ΔАВС , по св. острых углов. ∠СВА=90-35=55.