Question

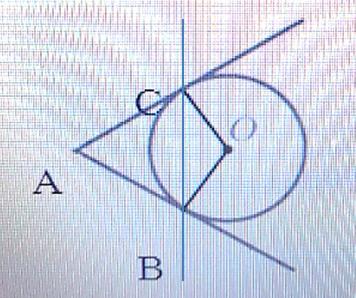
На рис 2 прямые АС и АВ касаются окружности с центром О в точках С и В соответственно. Найдите ∠АСВ, если ∠ВАС = 72°.

Answer 1

Ответ:

∠ACB = 54°

Объяснение:

По условию прямые АС и АВ касаются окружности, следовательно, прямые АС и АВ являются касательными к окружности. Так как касательные АС и АВ проведены из одной точки, то по свойствам касательных отрезки АВ и АС равны.

Проведём прямую СВ (см. рисунок) и получим треугольник ACB с равными боковыми сторонами АВ и АС, то есть треугольник ACB равнобедренный. По свойству равнобедренных треугольников углы при основании, в нашем случае ∠ABC и ∠ACB, равны.  

Так как сумма всех внутренних углов треугольника равна 180°, то  

∠ВАС= 180°–∠ACB–∠АВС.

Отсюда, в силу ∠ACB=∠АВС, ∠ВАС= 180°–2•∠ACB

или ∠ACB =(180°–∠ВАС)/2=(180°–72°)/2= 108°/2 = 54°.