Предмет: Алгебра,
автор: bohbel1
cos^2x + 4sinx + 4 =0
Ответы
Автор ответа:
2
Ответ:
x= - п/2 +2пk, k є Z
Объяснение:
cos^2x + 4sinx + 4 = 0
1 - sin^2x + 4sinx + 4 = 0
5 - sin^2x + 4sinx = 0
Нехай sinx = t. Тоді:
5 - t^2 + 4t = 0
- t^2 + 4t + 5 = 0 | - 1
t^2 - 4t - 5 = 0
t = - 1
t = 5
Підставляємо t в р-ння:
sinx = -1
sinx = 5 (тут нема розв'язку, бо синус лежить в межах від - 1 до 1)
x = - п/2 +2пk, k є Z
Приложения:
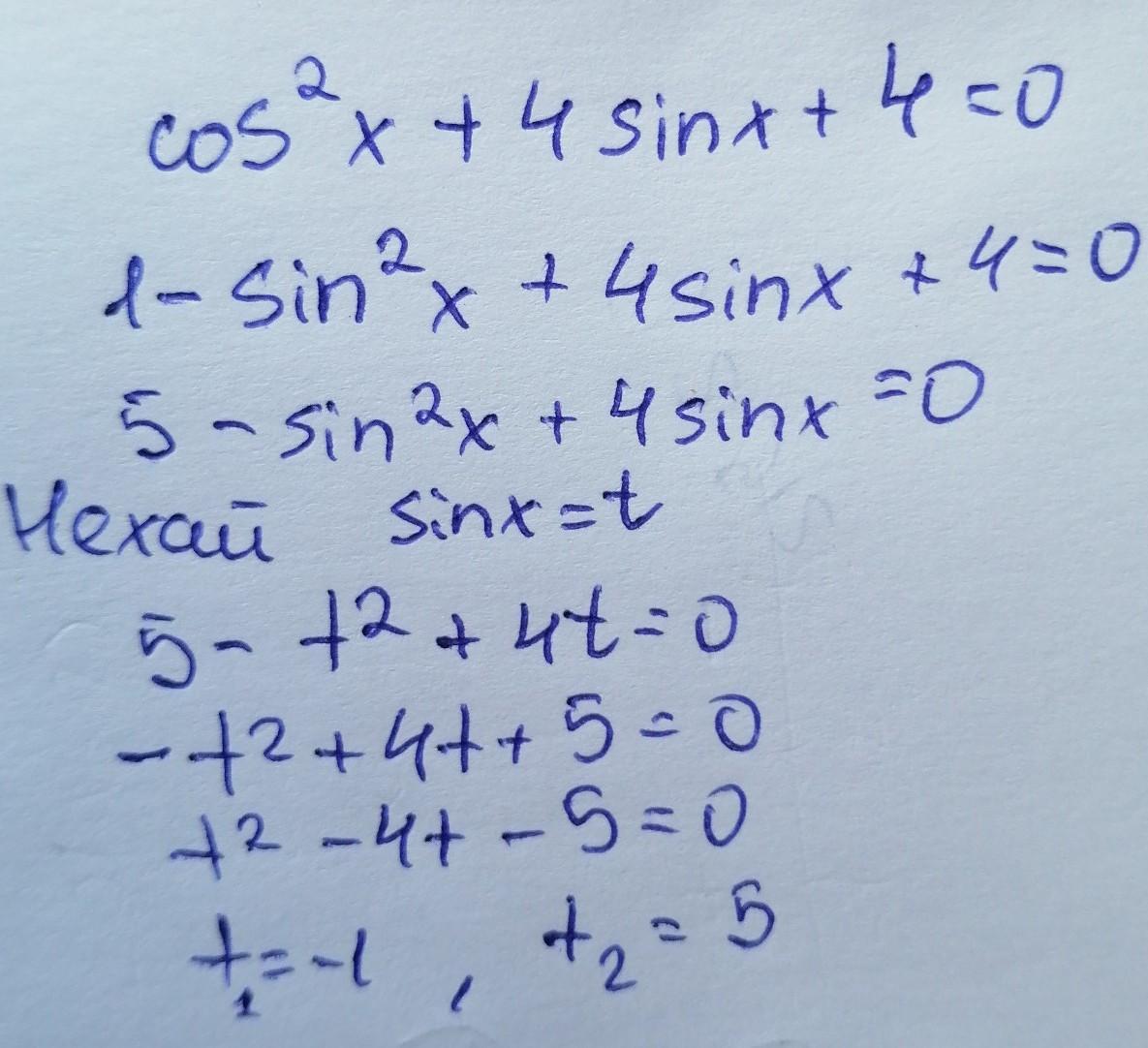
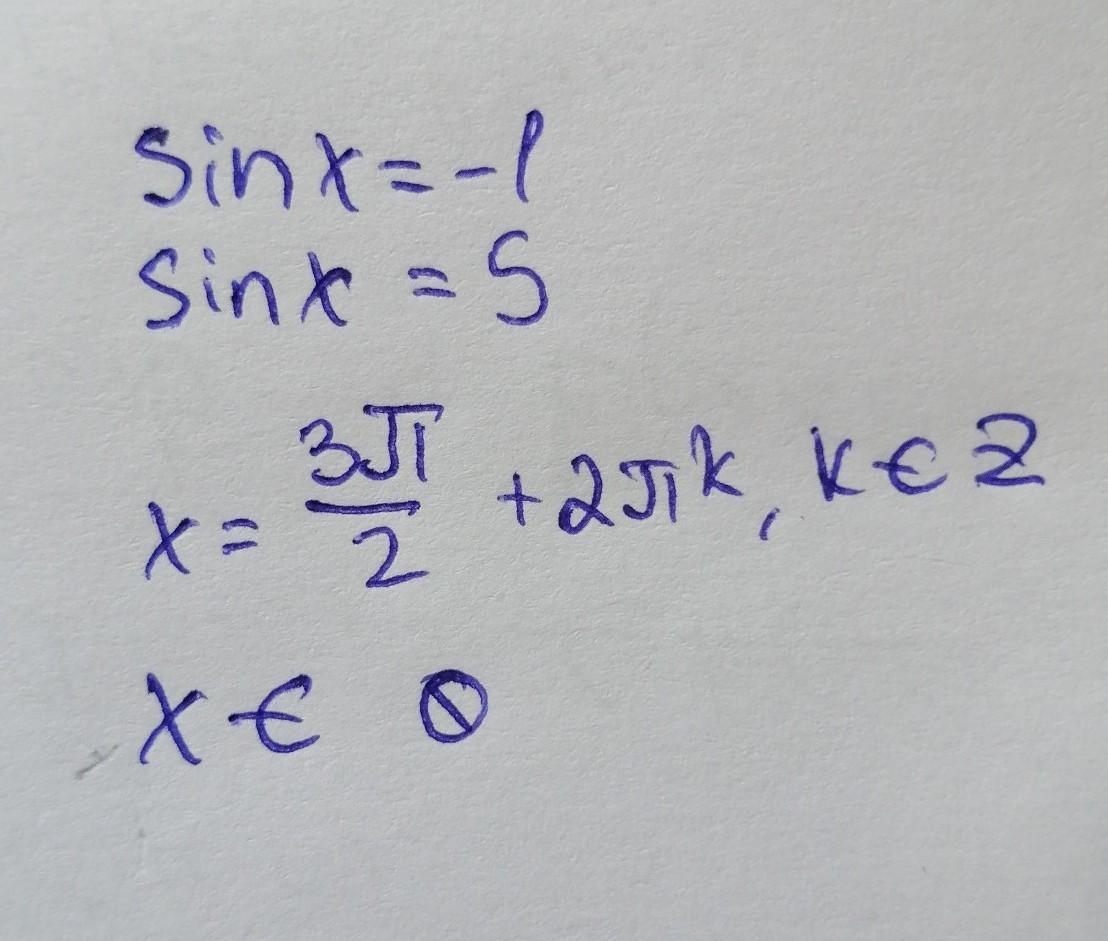
Похожие вопросы
Предмет: Химия,
автор: Revein
Предмет: Алгебра,
автор: bserega
Предмет: Алгебра,
автор: Neoo79
Предмет: Алгебра,
автор: jannaB
Предмет: Математика,
автор: КошечкаТВ