Question

Помогите пожалуйста ​

Answer 1

Ответ:

Пошаговое объяснение: Пусть 1 доля  диагонали х, тогда одна диагональ 3х, а другая 4х. Если периметр 100, то сторона 25, т.к. стороны у ромба равны. Используя свойство ромба Сумма квадратов диагоналей равна квадрату стороны, умноженной на 4, запишем уравнение:

(3x)²+(4x)²=4·25²

9x²+16x²=4·25²

25x²=4·25²

x²=4·25=100

x=10 Одна диагональ 3·10=30, другая 4·10=40

Используем еще свойства площади ромба:

с одной стороны она равна половине произведения диагоналей,

с другой - произведению стороны на высоту.

S=1/2(30·40)

S=25·h  Приравняем правые стороны и решим уравнение:

1/2(30·40)=25·h

600=25·h

h=600÷25

h=24

Answer 2

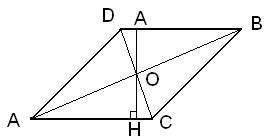
(У нас есть ромб со сторонами ABCD, смотр. Рис.)
Так как в ромбе все стороны равны, то периметр ромба равен
4x=100
x=25
То есть сторона ромба равна 25.
Учитывая, что диагонали ромба пересекаются под прямым углом, то треугольник AOC—прямоугольный с катетами AO=4x и OC=3x. Пользуясь теоремой Пифагора имеем:
AC^2=AO^2+OC^2
25=16x^2+9x^2
625=25x^2
x^2=25
x=+-5
Получаем длину катетов AO=4*5=20 и OC=3*5=15, Соответственно диагонали ромба равны 40 и 30.

Теперь найдём высоту AH из формул площади ромба.
S=d1*d2/2=AC*AH
(половина произведения диагоналей равно произведению стороны на высоту)

600=25*AH
AH=600/25=24

Ответ: 24