Предмет: Алгебра,
автор: uliafedotova667
решите пожалуйста, алгебру
Приложения:
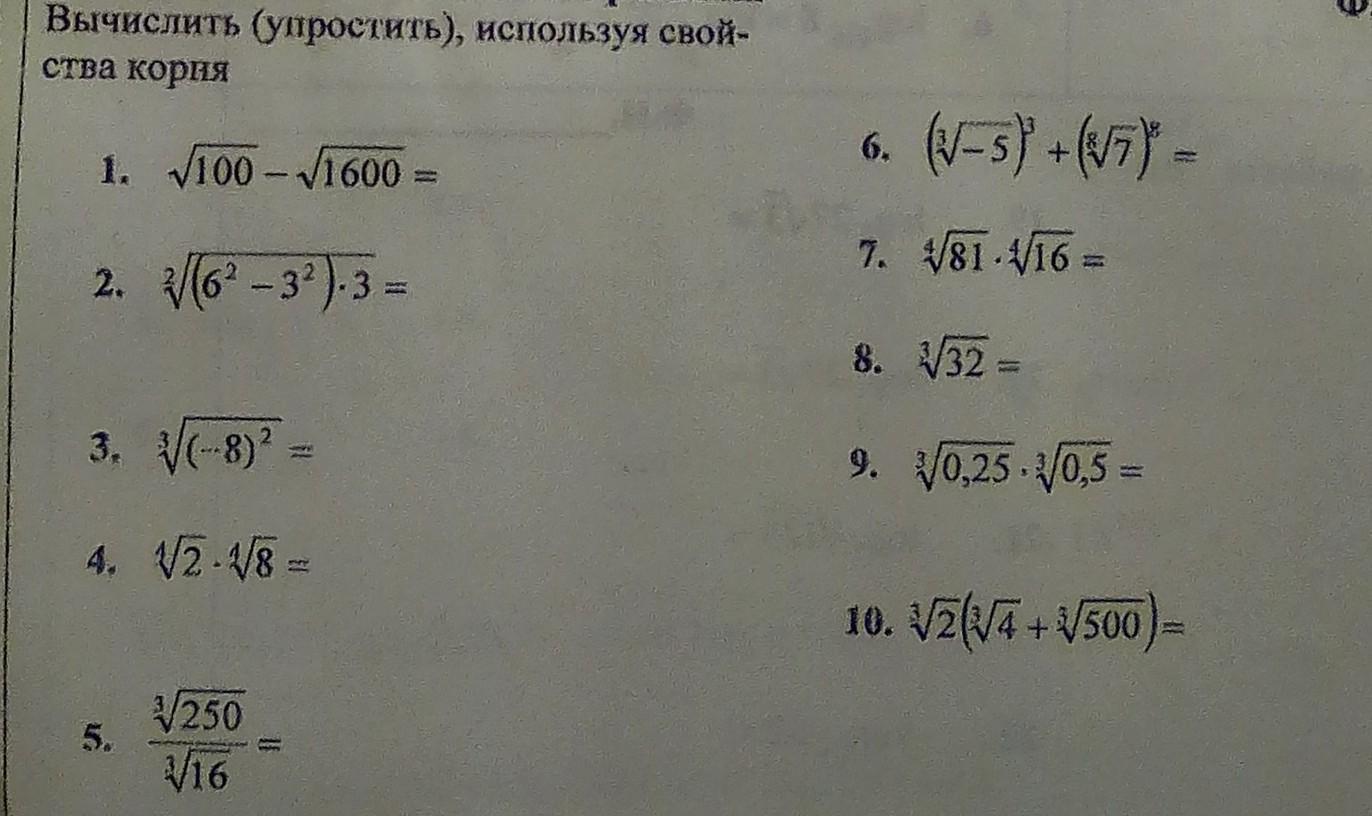
Ответы
Автор ответа:
1
Ответ:
1)
2) Вычисляем степень
Считаем, умножаем
3) Используя свойство корней напишем
Вычислим кубический корень
4) Произведение корней
5) Упростим выражение =
Вычислим корни =
6) Сокращаем показатели корня и степени, получаем
7) Упростим корень
Используем правило вычисления корней
Сократим степень и показатель корня
8) Вычислим произведение корней
Преобразуем в дробь
Вычислим кубический корень =
9) Упростим корень
Приведем подобные члены =
Вычислим произведение
Вычислим кубический корень
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: shirazz
Предмет: Английский язык,
автор: Vikulisa
Предмет: Математика,
автор: alexadeutscher
Предмет: Математика,
автор: марина03082