Предмет: Алгебра,
автор: Ggfyb24
Прошу решите интегралы!
Приложения:
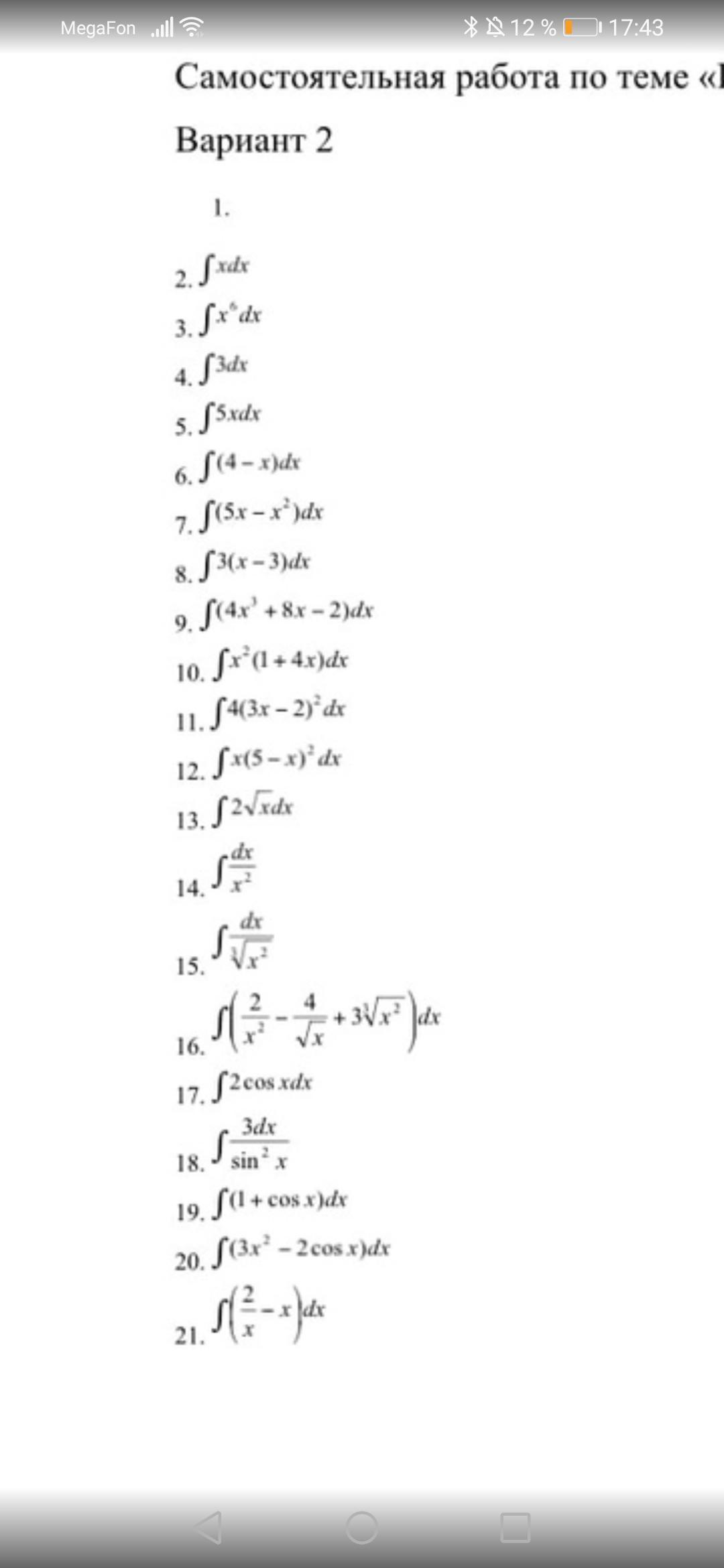
Ответы
Автор ответа:
2
Ответ:
2. ∫xdx=+C
3. ∫dx=
+C
4. ∫3dx=3x+C
5.∫5xdx=+C
6. ∫(4-x)dx=4∫dx-∫xdx=4x-+C
7. ∫(5x-)dx=5∫xdx-∫
dx=
8. ∫3(x-3)dx=∫(3x-9)dx=3∫xdx-9∫dx=
9.∫ 4∫
dx+8∫xdx-2∫dx=
10. ∫ ∫
∫
+4∫
=
11. ∫∫4 ×
dx=∫(36
-48x+16)dx=36∫
dx-48∫xdx+16∫dx=
=
12. ∫dx=∫
=∫
dx-10∫
dx+25∫xdx=
13.∫
14. ∫
15. ∫= ∫
dx=
16.∫=∫
=∫
dx-∫
dx+∫3
dx= -
17.∫2cosxdx=2∫cosxdx=2sinx+C
18.∫=3×∫
dx=-3ctgx+C
19. ∫(1+cosx)dx=∫dx+∫cosxdx=x+sinx+C
20.∫3-2cosx)dx=3∫
dx-2∫cosxdx=
21. ∫dx=∫
dx-∫xdx=2㏑(|x|)-
+C
Похожие вопросы