Предмет: Геометрия,
автор: katyacandy
Даю 30 баллов.
В треугольнике ABC A(2;1;3) , B(2;1;5), C(0;1;1). Найдите длину медианы Ам.
С решением, пожалуйста .
Ответы
Автор ответа:
1
Ответ:
Длина медианы АМ равна 1 .
Объяснение:
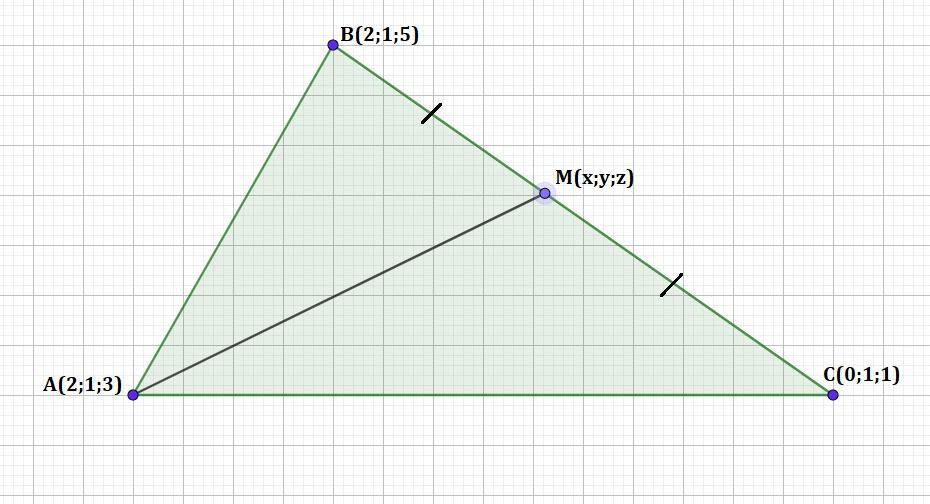
В треугольнике ABC A(2;1;3) , B(2;1;5), C(0;1;1). Найдите длину медианы АМ.
- Медиана треугольника – отрезок, проведенный из вершины треугольника, соединяющий эту вершину с серединой противолежащей стороны треугольника.
АМ - медиана ΔАВС. Следовательно точка М - середина стороны ВС.
Найдём координаты точки М(x;y;z).
- Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Таким образом координаты точки М(1;1;3).
Длину медианы АМ находим по формуле длины отрезка:
Длина медианы АМ равна 1.
#SPJ5
Приложения:
Похожие вопросы
Предмет: История,
автор: saraaktanzholaman
Предмет: Алгебра,
автор: SergeyMedovnik
Предмет: Литература,
автор: flippa
Предмет: Математика,
автор: тыква4