Предмет: Геометрия,
автор: artem48239
В прямоугольном треугольнике проведена высота к гипотенузе.
Какие углы эта высота образует с катетами, если больший из острых углов этого треугольника равен 61°?
Боже, огромное спасибо за коронку :3
Ответы
Автор ответа:
1
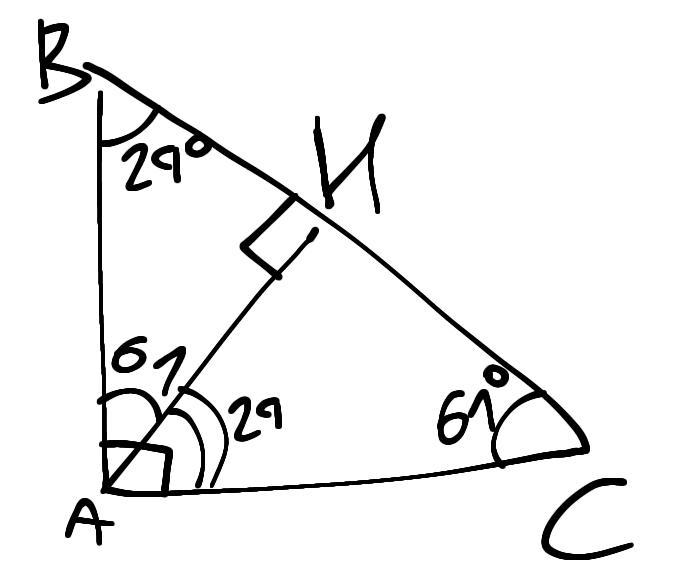
Высота, проведенная к гипотенузе, делит прямоугольный треугольник на два прямоугольных треугольника, каждые из которых подобен друг другу и искомому большому прямоугольному треугольнику.
Тоесть, ∆ABH ~ ∆AHC ~ ∆ABC
А как знаешь, у подобных треугольников соответственные углы равны.
Приложения:
1. Угол с меньшим катетом равен
°.
2. Угол с большим катетом равен
°.
°.
2. Угол с большим катетом равен
°.
Угол у большего катета равен 29°, а у меньшего 61°
Автор ответа:
0
Ответ:
ADB=61°, BDC=29°
Объяснение:
по скольку DB-высота она образует со стороной прямой угол
тогда угол DBC =90°
по скольку сума углов треугольника равна 180°
то
угол BDC=180°-(90°+61°)=29°
по скольку угол ADC прямой то угол
ADB=90°-29°=61°
Приложения:
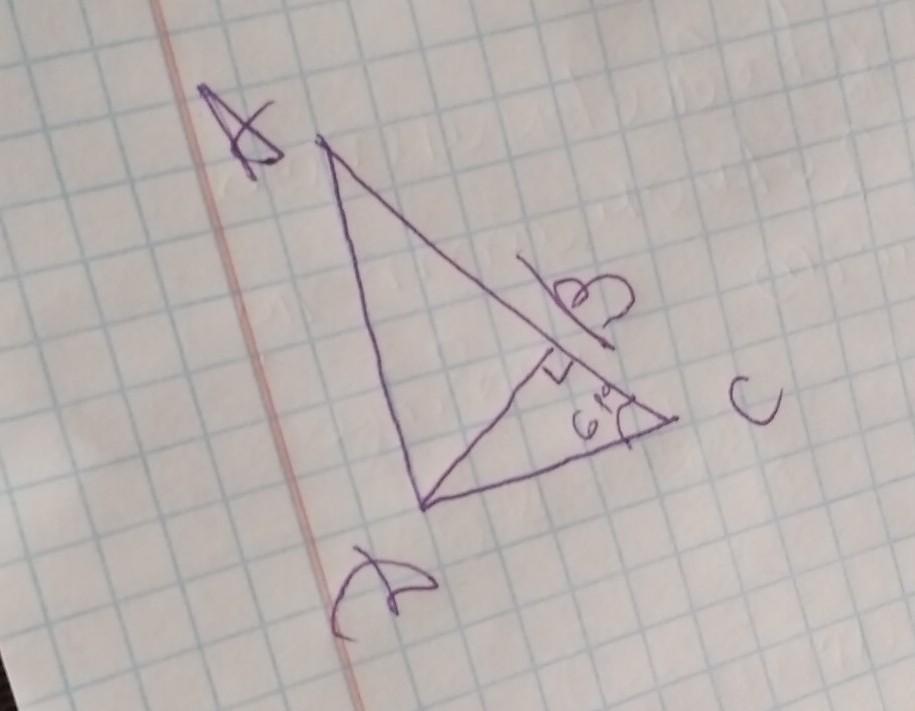
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: nyashec
Предмет: Геометрия,
автор: ZuZyanya
Предмет: Математика,
автор: kmimimi
Предмет: Математика,
автор: 683837362
°.
2. Угол с большим катетом равен
°.