Предмет: Алгебра,
автор: avakindara8
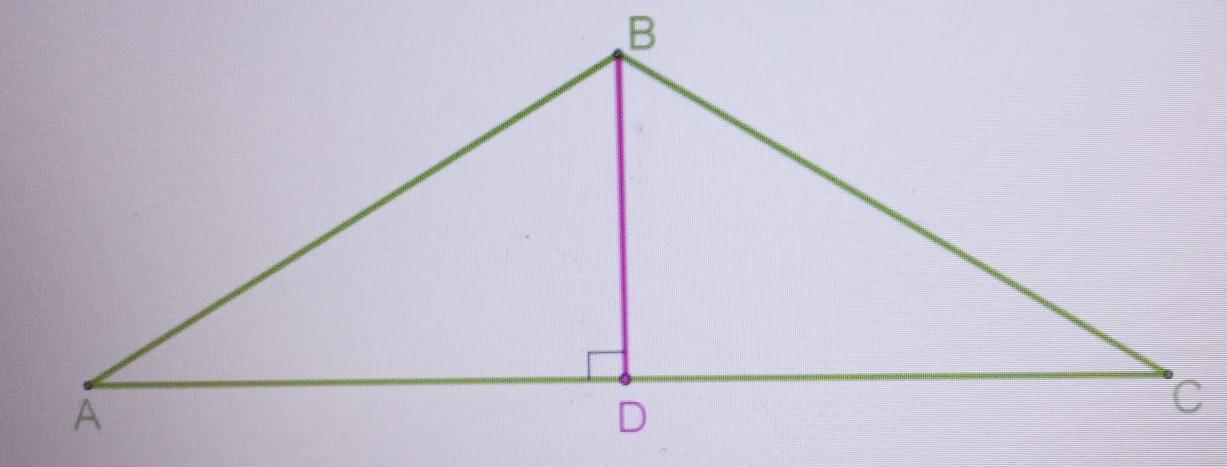
Вравнобедренном треугольнике ABC проведена высота BD к основанию АС.
Длина высоты — 5,8 см, длина боковой стороны — 11,6 см.
Определи углы этого треугольника.
угол BAC =
угол BCA =
угол ABC =
Приложения:
Ответы
Автор ответа:
6
Ответ:
ВАС = 30°;
ВСА = 30°;
АВС = 120°.
Объяснение:
Высота разбивает равнобедренный треугольник на 2 прямоугольных равных между собой.
В прямоугольном ΔABD катет ВD = 5,8 см, а гипотенуза АВ = 11,6 см.
Если 11,6 см : 5,8 см = 2
Получается, что катет равен половине гипотенузы, а это возможно если этот катет лежит против угла в 30°.
ВАС = ВСА = 30°.
Сумма всех углов треугольника всегда равна 180°.
Отсюда:
АВС = 180° - (30° + 30°) = 120°.
ВАС = 30°;
ВСА = 30°;
АВС = 120°.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: Аноним
Предмет: Геометрия,
автор: dasha2611
Предмет: Математика,
автор: ALEX2010Q