Question

решите системы уравнений графическим способом
1,5x-y=0
x+y+5=0
пж помогите!

Answer 1

Решение:

Чтобы найти точку пересечения данной системы уравнений нужно перенести все члены каждого из уравнений в правую часть со сменой знака, а в левой части оставить переменную $y$.

$\left \{ {{1,5x-y=0} \atop {x+y+5=0}} \right. \Rightarrow \left \{ {{-y=0-1,5x \: \: |\cdot (-1)} \atop {y=-5-x}} \right. \Rightarrow \left \{ {{y=0+1,5x} \atop {y=-5-x}} \right.$

Теперь необходимо составить таблицу для переменных $x$ и $y$, чтобы можно было подставлять значения выражений. После этого мы чертим координатную плоскость и находим точку пересечения прямых.

$1:\left[\begin{array}{ccc}x&y\\2&3\\4&6\end{array}\right] 2:\left[\begin{array}{ccc}x&y\\-5&0\\-3&-2\end{array}\right]$

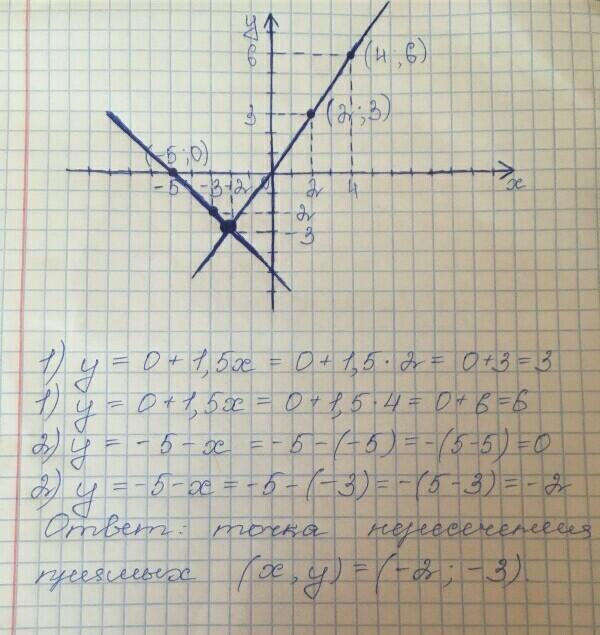
График прикреплён. Точка пересечения указана внизу.

Ответ:   $\boxed{\bf \Big(x; \: y\Big)=\Big(-2; \: \: -3\Big)}$