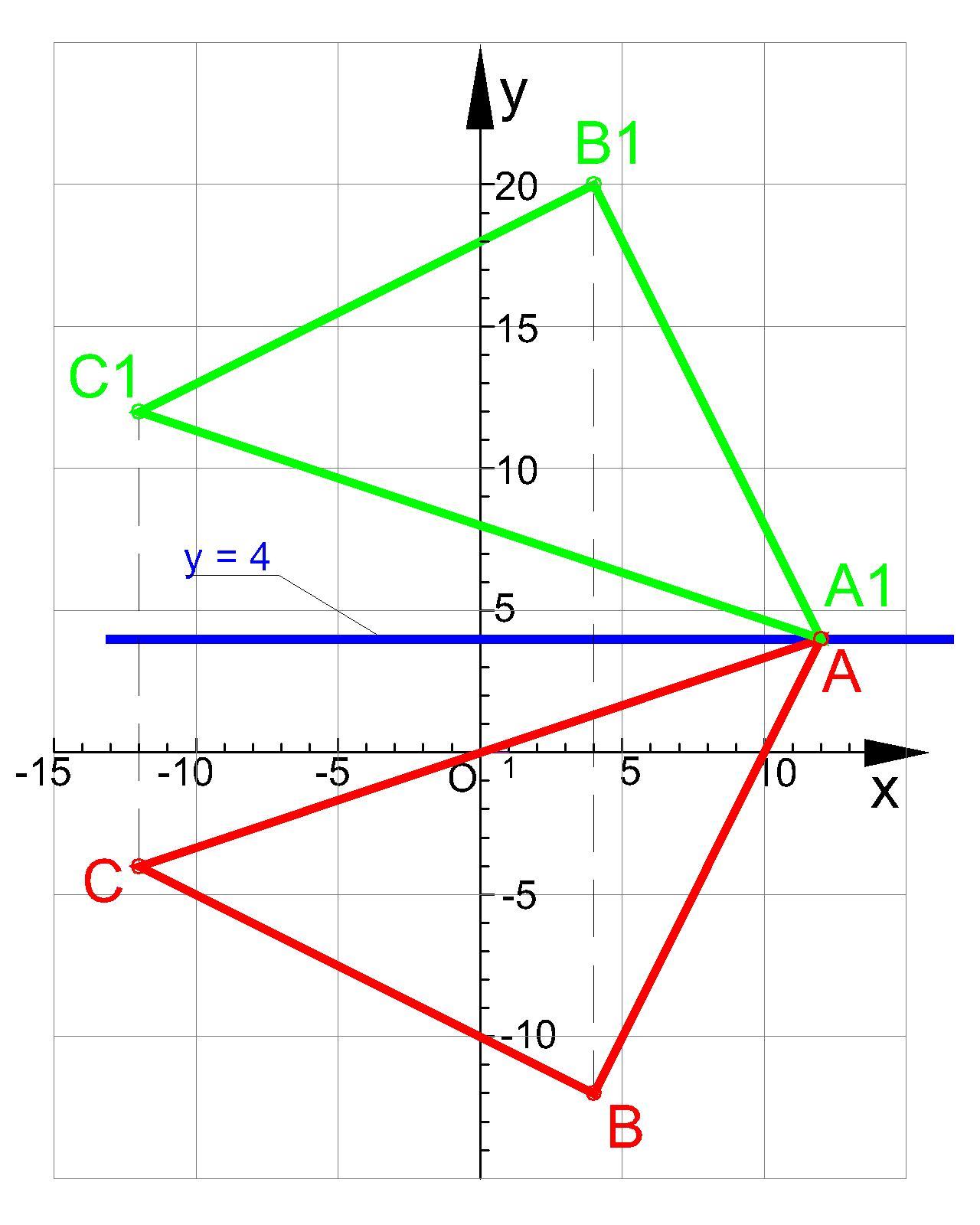
На координатной плоскости построй треугольник, вершинами которого являются точки:
A (12, 4), B (4; -12) и C (-12; -4).
Нарисуй треугольник A1B1C1, симметричный данном относительно прямой y = 4.
Напиши координаты вершин треугольника A1B1C1:
Ответы
Ответ:
А1(12;4) , В1(4; 20) , С1(-12; 12).
Объяснение:
1. Выполняем построение треугольника АВС.
2. Строим график прямой у = 4 . Это горизонтальная прямая проходящая через точку (0; 4)
3. Выполняем построение симметричной фигуры:
Т. А совпадает с точкой А1, т.к. ордината т. А = 4 и лежит на прямой у = 4.
от т. В проводим перпендикуляр к прямой у = 4. Откладываем перпендикуляр такой же длины в противоположною сторону от прямой у = 4.
То же самое выполняем для т. С.
Координаты ΔA1B1C1 можно определить графически:
А1(12;4) , В1(4; 20) , С1(-12; 12).
Также ординаты симметричных точек можем определить математически:
у1 = 4 + (4-у) = 8-у.
Здесь 4 - это сдвиг координат вверх на 4 единицы, (4-у) - расстояние между осью симметрии и точками исходного треугольника.
Абсциссы остаются неизменными, т.к. ось симметрии - горизонтальная.