Предмет: Математика,
автор: ississiiei
тригонометртчекие уравнения решите пожалуйста
Приложения:
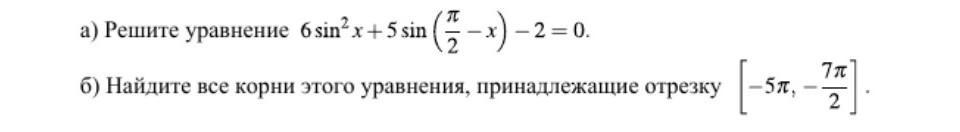
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:

Автор ответа:
1
Ответ:
Пошаговое объяснение:
Воспользуемся формулами приведения.
"Так как под знаком преобразуемой тригонометрической функции содержится выражение (π/2 — x), то наименование тригонометрической функции меняем на родственное, т. е. синус — на косинус."
Воспользуемся основным тригонометрическим тождеством:
Введем новую переменную, пусть cosx = a, тогда получим
Вернемся к первоначальной переменной, получим два уравнения.
Решим 1 уравнение:
cosx = 4/3
Уравнение не имеет решения, так как — 1 ≤ cosx ≤ 1.
Решим 2 уравнение:
cosx = - 1/2
Похожие вопросы
Предмет: Физика,
автор: bloom1999r
Предмет: Геометрия,
автор: ardon
Предмет: География,
автор: aibarrr
Предмет: География,
автор: dery4g
Предмет: Математика,
автор: izotoff2011