Предмет: Математика,
автор: AmelyLakrua
Помогите решить два определённых интеграла, пожалуйста.
Приложения:
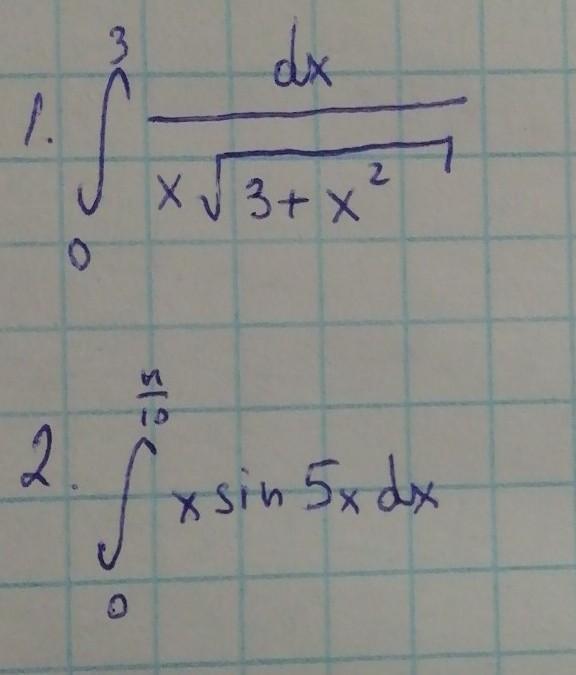
Ответы
Автор ответа:
1
Интеграл расходится
AmelyLakrua:
большое вам спасибо!
Похожие вопросы
Предмет: Биология,
автор: cocos0
Предмет: Обществознание,
автор: Фейхуа
Предмет: История,
автор: happy2000arina
Предмет: Математика,
автор: nata5081
Предмет: Математика,
автор: adilxanova81