Предмет: Алгебра,
автор: kakto97
упростить выражение
cos^2(a-(pi/6))-cos^2(a+(pi/6))
Приложения:
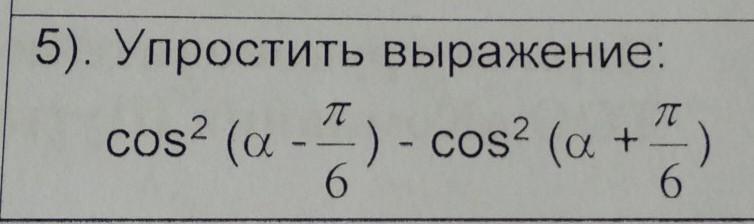
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Аnna23
Предмет: Математика,
автор: alin4ik112
Предмет: Геометрия,
автор: CallMeMaybe
Предмет: Алгебра,
автор: Stepashka18
Предмет: Алгебра,
автор: шолпан18