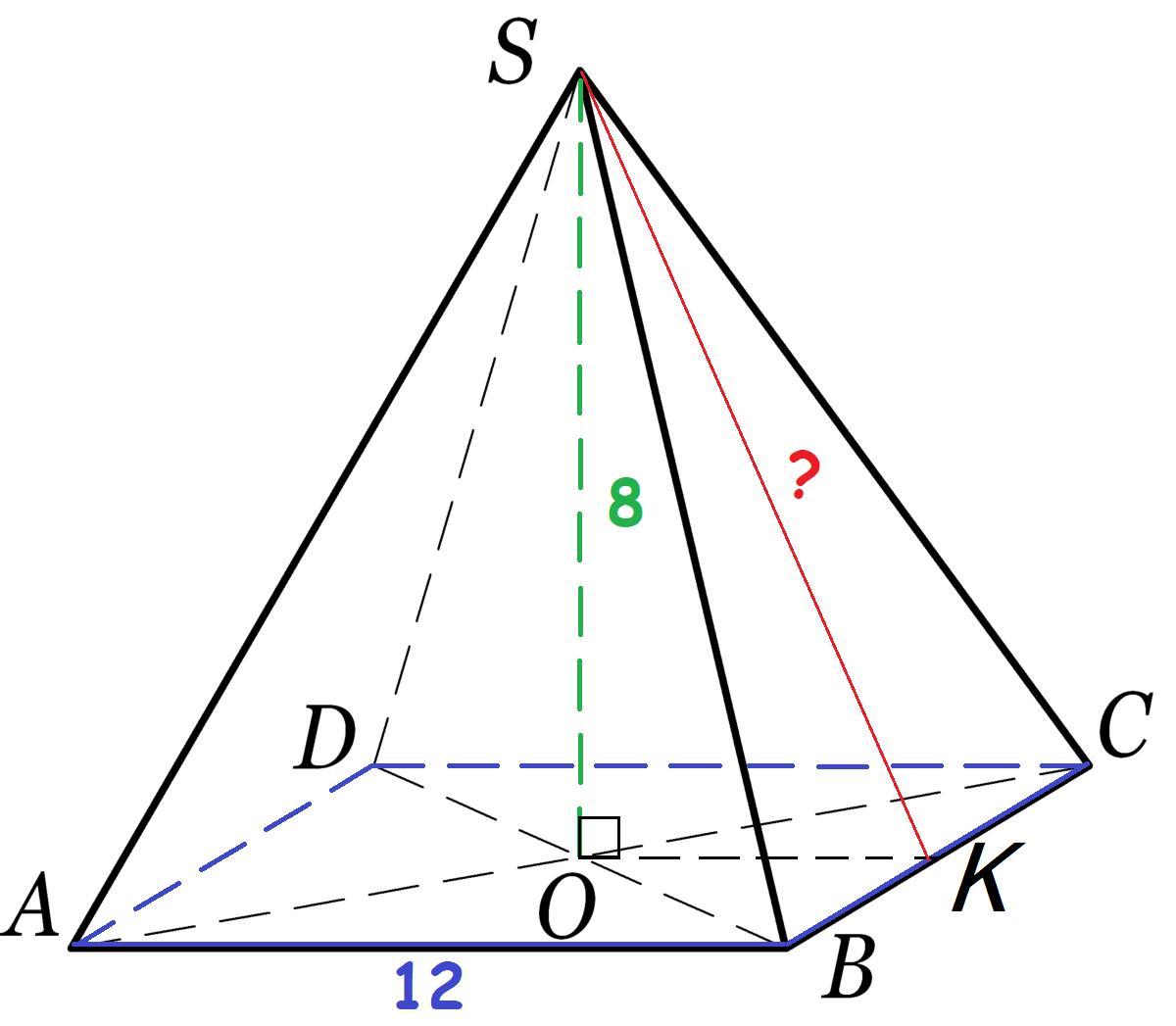
По стороне основания 12 и высоте 8 найдите апофему правильной четырёхугольной пирамиды.
Ответы
Дано:
Правильная четырёхугольная пирамида.
Сторона основания = 12.
Высота пирамиды = 8.
Найти:
Апофема пирамиды - ?
Решение:
Обозначим правильную четырёхугольную пирамиду буквами SABCD.
AB - сторона основания ⇒ AB = 12.
SO - высота пирамиды ⇒ SO = 8.
Т.к. данная пирамида - правильная четырёхугольная ⇒ основание этой пирамиды - квадрат.
Квадрат - это геометрическая фигура, у которой все стороны равны.
⇒ АВ = ВС = CD = AD = 12.
Обозначим точку К на стороне ВС.
Проведём апофему SK из вершины пирамиды S к точке К.
Апофема - высота боковой грани правильной пирамиды, проведённая из вершины этой пирамиды.
Апофема, проведённая из вершины правильной пирамиды к стороне основания этой пирамиды, делит эту сторону на две равные части.
Катет прямоугольного треугольника, образованный апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины стороны основания правильной пирамиды.
ОК - образованный катет ⇒ ОК = 1/2AB(CD, AD, BC) = 12/2 = 6.
ΔSOK - прямоугольный, так как SO - высота пирамиды.
Найдём апофему SK, по теореме Пифагора: (с = а² + b², где с - гипотенуза; a, b - катеты).
SK = √(SO² + OK²) = √(8² + 6²) = √(64 + 36) = √100 = 10 ед.
Ответ: 10 ед.