Question

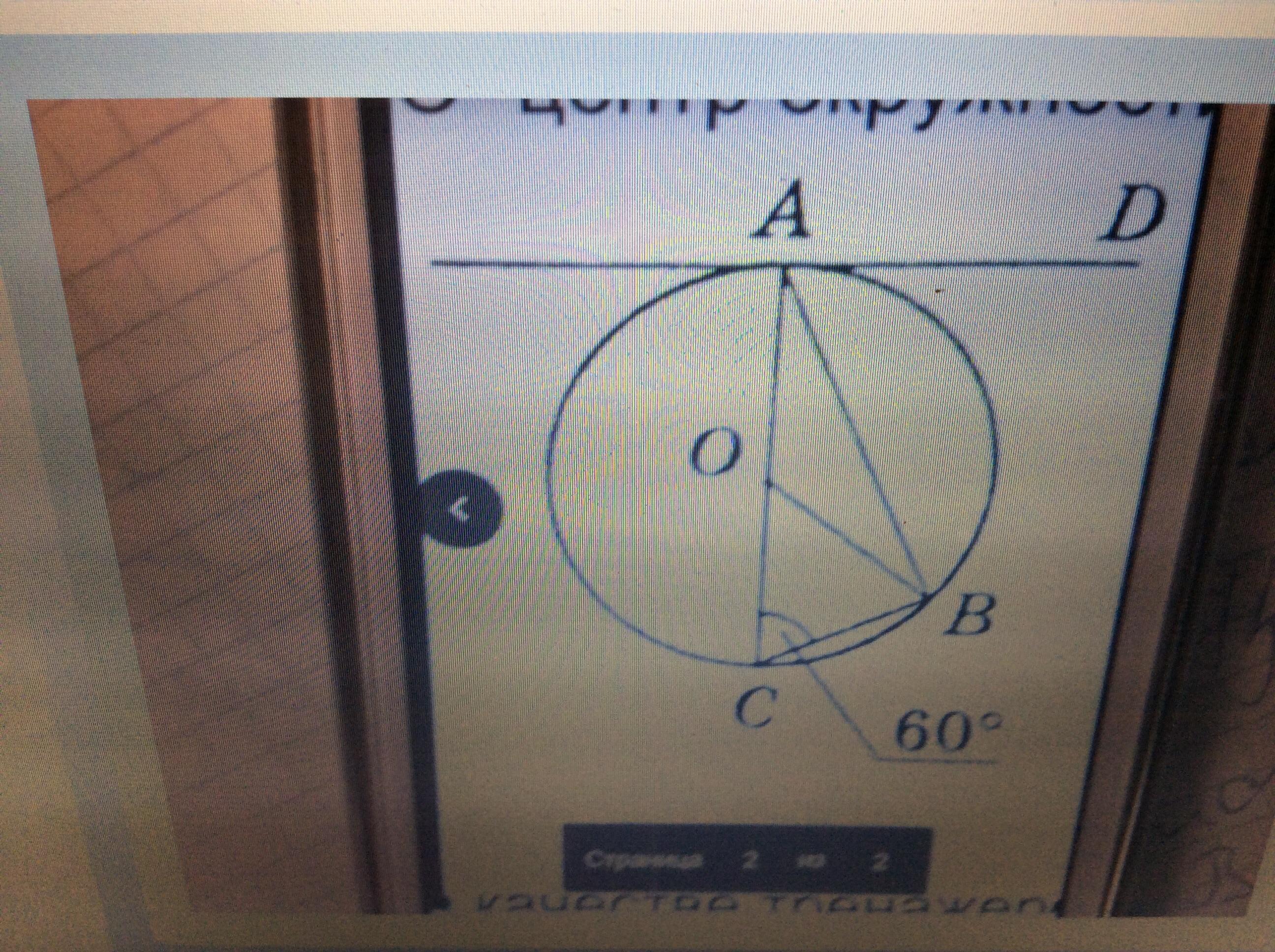
O- центр окружности, АD- касательная к окружности. Найти угол DAB. ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!!!!!!!!!

Answer 1

Ответ:

Касательная перпендикулярна радиусу ОА.

Рассмотрим треугольник АОВ-равнобедренный=>(180°-120°):2=30°-<ОВА=<ОАВ

90°-30°=60°-<BAD

Answer 2

ΔОСВ равносторонний. В нем углы при вершинах С и В равны.т.к. ОС=ОВ= радиусы одной окружности. Т.е.  равнобедренный получается. но поскольку углы С и В еще и по 60°в, то и угол О в этом треугольнике 60 °. Тогда  внешний угол АОВ равен сумме двух внутренних ∠ В и ∠С, с ним не смежными, т.е. он равен 60°+60°=120°, а тогда в равнобедренном треуг. АОВ ∠ А =∠ В= 30 °,

(180°-120°)/2=30°,  как углы при основании равнобедренного ΔАОВ, т.к. АО и ВО радиусы одной окружности и ∠DАС = 90°, т.к. радиус, проведенный в точку касания перпендикулярен касательной АD, значит, искомый  ∠ DАВ =90°-30°=60°

Ответ 60 °