Предмет: Математика,
автор: lil290464
Исследуйте функцию на монотонность, точки экстремума:
1. y=3x^4-4x^3
2. y=60+45x-x^3-3x^2
Желательно с графиком
Приложения:
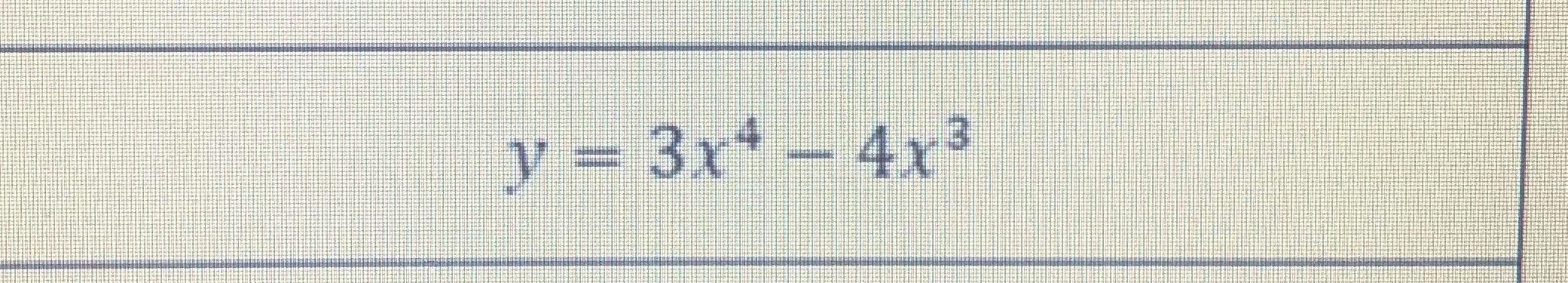

Ответы
Автор ответа:
1
Ответ: Находим первую производную функции:
или
Приравниваем ее к нулю:
Вычисляем значения функции
Ответ:
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
или
Вычисляем:
- значит точка
точка перегиба функции.
- значит точка
точка минимума функции.
Похожие вопросы
Предмет: Обществознание,
автор: владуся12
Предмет: Математика,
автор: Елизабет1
Предмет: Другие предметы,
автор: Ддаашка
Предмет: Литература,
автор: юляша5а