Предмет: Алгебра,
автор: 245689999
Решите пожалуйста очень срочно дам 100 баллов
Приложения:
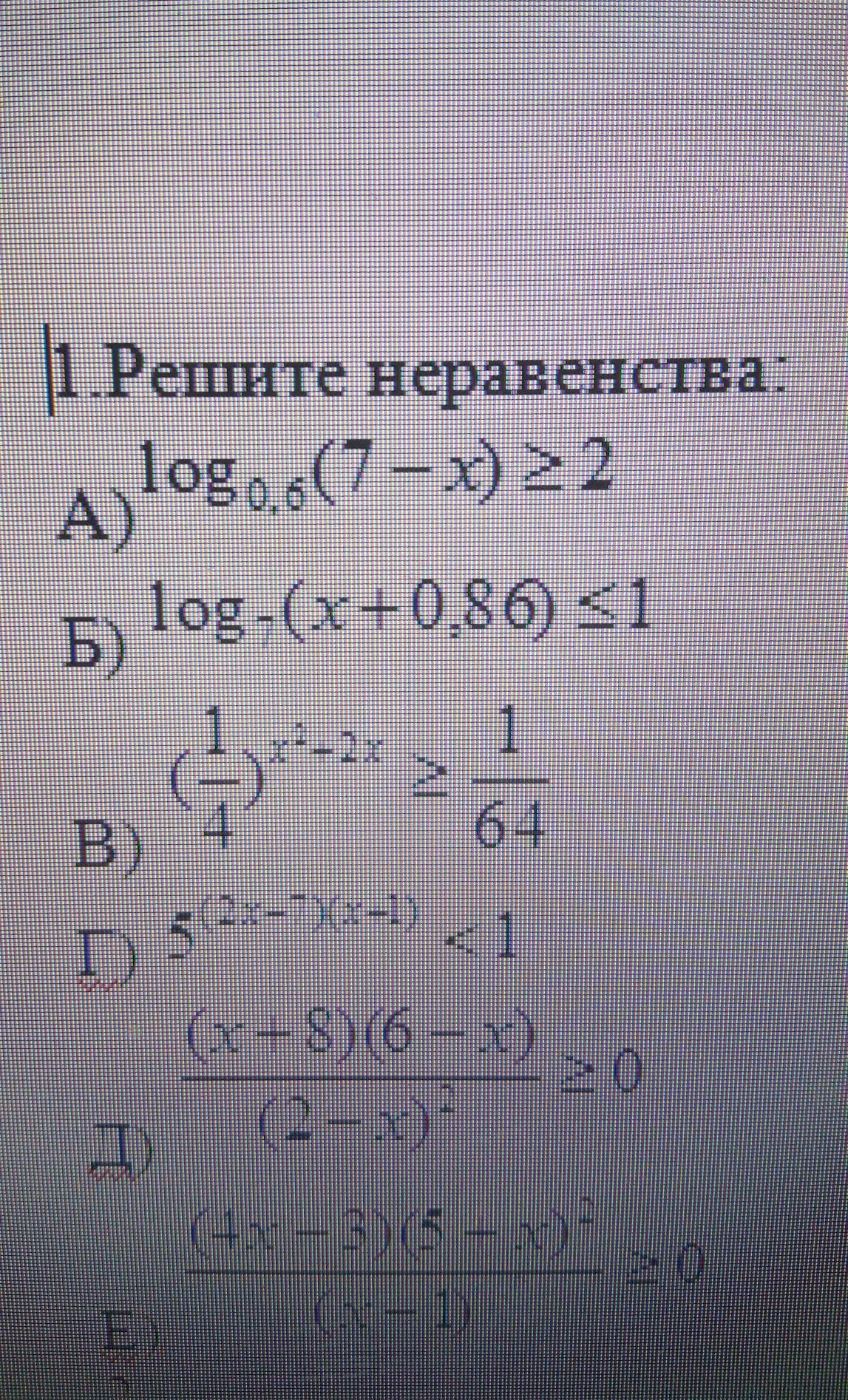
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Ответ: x∈[6,64;7).
Б)
Ответ: х∈(-0,86;6,14]
B)
Г)
-∞__+__-1__-__3,5__+__+∞
x∈(-1;3,5).
Д)
-∞_-_(2)_-_6__+__8__-__+∞
x∈[6;8].
sangers1959:
Удачи.
помогите мне с корнями
заранее спасибо
Давайте задание.
снйчас задам
я задала
Там занято.
Две пишут. Пускай решат.Я проверю.
хорошо
уже написал 1 второго нету можете ответить
Похожие вопросы
Предмет: Русский язык,
автор: nasty2711
Предмет: Русский язык,
автор: Аноним
Предмет: Биология,
автор: Cataina
Предмет: Геометрия,
автор: миа16
Предмет: Математика,
автор: ser4okey