Помогите пожалуйста
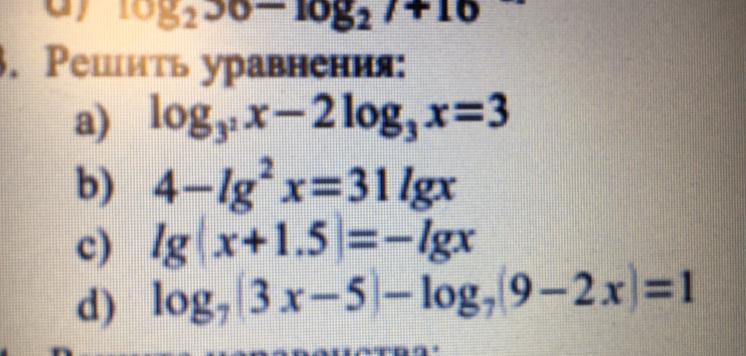
Ответы
Ответ:
Объяснение:
a)
log₃²(x)-2*log₃(x)=3 ОДЗ: x>0 ⇒ x∈(0;+∞)
(1/2)*log₃x-2*log₃x=3
-(3/2)*log₃=3 |×(-2/3)
log₃x=-2
x=3⁻²=1/3²
x=1/9 ∈ОДЗ.
Ответ: х=1/9.
b)
4-lg²x=3*lgx ОДЗ: x>0 ⇒ x∈(0;+∞).
lg²x+3*lgx-4=0
Пусть lgx=t ⇒
t²+3t-4=0 D=25 √D=5
t₁=lgx=-4 ⇒ x=10⁻⁴=0,0001
t₂=lgx=1 ⇒ x=10¹=10.
c) lg(x+1,5)=-lgx ОДЗ: x+1,5>0 x>-1,5 x>0 ⇒ x∈(0;+∞).
lg(x+1,5)+lgx=0
lg((x+1,5)*x)=0
x²+1,5x=10⁰=1
x²+1,5x-1=0 D=6,25 √D=2,5
x₁=-2 ∉ОДЗ x₂=0,5 ∈ОДЗ.
Ответ: х=0,5.
d)
log₇(3x-5)-log₇(9-2x)=1
ОДЗ: 3x-5>0 3x>5 x>5/3 9-2x>0 2x<9 x<4,5 ⇒ x∈(5/3;4,5).
log₇(3x-5)-log₇(9-2x)=log₇7
log₇(3x-5)-log₇(9-2x)-log₇7=0
log₇((3x-5)/(7*(9-2x))=0
(3x-5)/(7*(9-2x))=7⁰
(3x-5)/(63-14x))=1
3x-5=63-14x
17x=68 |÷17
x=4 ∈ОДЗ.
Ответ: х=4.