Предмет: Геометрия,
автор: sasaantonova2222
В равнобедренном треугольнике ABC проведена высота BD к основанию AC.
Длина высоты — 6,9 см, длина боковой стороны — 13,8 см.
Определи углы этого треугольника.
Ответы
Автор ответа:
5
Ответ:
Т.к. треуг. равнобедренный, то АВ=АС=13,8.
6,9*2=13,8. следовательно, это свойство(катет, лежащий против угла 30° равен половине гипотенузы). Значит угол С равен 30°.
Т.к. ВD- высота, то угол ВDС-прямой, равен 90°.
Сумма углов треуг. равна 180°, отсюда угол DBC равен 180-30-90=60°
Т.к. это равнобедренный тр., то высота является и биссектрисой тоже. Значит угол DBС равен углу DBA=60°
Весь угол АВС=60*2=120°
Угол А равен углу С= 30°(углы при основании)
Ответ: 30,30,120.
Приложения:
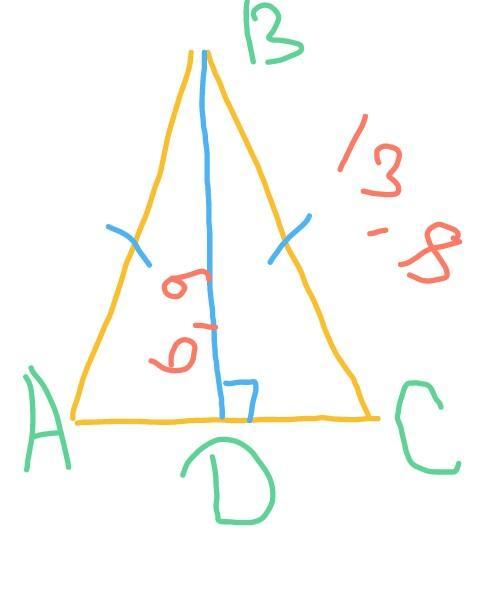
Похожие вопросы
Предмет: История,
автор: Arsen200020
Предмет: Русский язык,
автор: samvel2003
Предмет: Другие предметы,
автор: AnettaS
Предмет: Математика,
автор: дашуля267