Предмет: Математика,
автор: alina9kozlovskaya
Как такое решать ?Объясните пожалуйста.
Приложения:
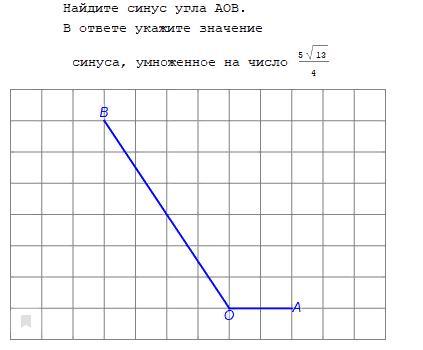
Ответы
Автор ответа:
0
Ответ:
1) sin AOB = 3/√13
2) 3,75
Пошаговое объяснение:
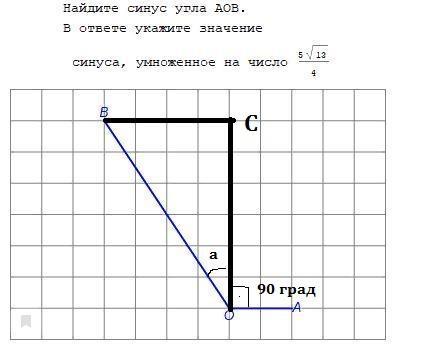
1) ∠AOB=∠AOC+∠COB
∠AOC=90°, ∠COB=α
∠AOB=90°+α
sinAOB =sin (90°+a) = cosα (формула приведения)
ΔOCB - прямоугольный ∠OCB=90°, OC=6, CB=4 =>
=> BO=√(OC²+CB²)= √(6²+4²)= √52 = √(4*13) = 2√13
cosα = OC/OB = 6/2√13 = 3/√13 (косинус острого угда прямоугольного треугольника равен отношению прилежащего катета к гипотенузе)
Значит, sin AOB = 3/√13
2) sinAOB * 5√13/4 = 3/√13 * 5√13/4 = 3*5/4 = 15/4 = 3,75
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: ЛЯЛЯМИТРОФАНОВА
Предмет: Алгебра,
автор: анька0561
Предмет: Математика,
автор: BelieberDusia
Предмет: Литература,
автор: anachanum4ik
Предмет: Математика,
автор: nikita741236987